Question

已知数列{a_n}的前三项依次为-2，2，6，且前n项和S_n是n的不含常数项的二次函数，则a₁₀₀=（ ）
A．394
B．392
C．390
D．396

Answer 1

【答案】分析：根据等差数列的前n项和的表达式得到数列{a_n}是等差数列，结合数列{a_n}的前三项-2，2，6，求出等差数列的通项公式进而得到答案．
解答：解：由题意可得：等差数列的前n项和的表达式为：，
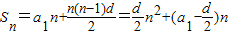
所以等差数列的前n项和的表达式是n的不含常数项的二次函数，
因为数列{a_n}的前n项和S_n是n的不含常数项的二次函数，
所以数列{a_n}是等差数列．
又因为数列{a_n}的前三项依次为-2，2，6，
所以数列的首项为-2，公差为4，
所以数列{a_n}的通项公式为：a_n=4n-6，
所以a₁₀₀=394．
故选A．
点评：解决此类问题的根据是熟练掌握等差数列的通项公式与前n项和的表达式，并且加以正确的运算．