
分析 求导,求出函数是单调函数时,实数a的取值范围,再求补集.
解答 解:函数f′(x)=$\frac{a}{x}+2x$+a-6.
①若函数f(x)=alnx+x2+(a-6)x在(0,3)上单调递增,
则f′(x)=$\frac{a}{x}+2x$+a-6≥0在(0,3)上恒成立,
即a≥$\frac{6x-2{x}^{2}}{x+1}$=-2[(x+1)+$\frac{4}{x+1}$-5]在(0,3)上恒成立,
函数g(t)=t+$\frac{4}{t}$,t∈(1,4),g(t)∈[4,5),∴a≥2;
②若函数f(x)=alnx+x2+(a-6)x在(0,3)上单调递减,
则f′(x)=$\frac{a}{x}+2x$+a-6≤0在(0,3)上恒成立,
即a≤$\frac{6x-2{x}^{2}}{x+1}$=-2[(x+1)+$\frac{4}{x+1}$-5]在(0,3)上恒成立,
函数g(t)=t+$\frac{4}{t}$,t∈(1,4),g(t)∈[4,5),∴a≤0.
则函数f(x 在(0,3)上不是单调函数,则实数a的取值范围是(0,2)
故答案为(0,2)
点评 本题的考点是利用导数研究函数的单调性,对于参数问题要注意进行分类讨论.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 20 | 80 |
| 北方学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,-$\frac{2}{3}$) | C. | (3,+∞) | D. | (-$\frac{2}{3}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.5 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有97.5%以上的把握认为“市民收入增减与旅游愿望无关” | |
| B. | 有97.5%以上的把握认为“市民收入增减与旅游愿望有关” | |
| C. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望无关” | |
| D. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 60 | ||
| 不肥胖 | 10 | ||
| 合计 | 100 |
| P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
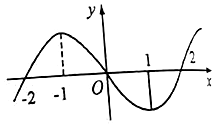 已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )
已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-∞,2)∪(2,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-2,-1)∪(1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com