
分析 ①根据回归直线方程的意义可以判断命题正确;
②根据残差图中残差点分布的意义即可判断命题错误;
③根据正态分布的计算方法,求出成绩在550~600分的人数约是多少;
④根据相关指数R2的意义,即可判断命题正确.
解答 解:对于①,回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量y增加0.1个单位,正确;
对于②,做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越好,②错误;
对于③,根据题意,考生成绩在550~600分的人数约为$\frac{1}{2}$(0.9544-0.6826)×25000≈3397,∴③正确;
对于④,相关指数R2=0.64,表示解释变量对预报变量的贡献率为64%,正确;
综上,正确的命题是①③④.
故答案为:①③④.
点评 本题考查了回归直线方程的应用问题,也考查了残差图以及正态分布的应用问题,相关指数R2的应用问题,是基础题目.


科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(理)试卷(解析版) 题型:选择题
几何体的三视图(单位:cm)如右上图所示,则此几何体的表面积是

A.90 cm2 B.129 cm2 C.132 cm2 D.138 cm2
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
若不等式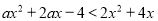 对任意实数x均成立,则实数a的取值范围是( )
对任意实数x均成立,则实数a的取值范围是( )
A.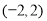 B.
B.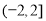
C. D.
D.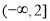
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com