解:(Ⅰ)∵EC⊥平面ABD,
∴V=

CE.S
ABD=

…4分
证明:(Ⅱ)连接A
1C
1,在正方体ABCD-A
1B
1C
1D
1中
B
1D
1⊥A
1C
1,B
1D
1⊥CC
1,A
1C
1∩CC
1=C
1∴B
1D
1⊥面A
1C
1CA,
AE?面A
1C
1CA
∴B
1D
1⊥AE…8分
(Ⅲ)证法一:连接AC
1,取AC
1的中点为H,取AC的中点O,连接HO,
∵HO∥EC且HO=EC
∴四边形HOCE为平行四边形,OC∥HE即AC∥HE---------13’
连接BD
1,易知四边形A
1BCD
1为平行四边形,则H为BD
1和A
1C的交点
∴HE?平面B
1DE
AC?平面B
1DE
AC∥平面B
1DE…12分
证法二:延长BC与B
1E延长线交于F,连DF∵E为棱CC
1中点
∴△B
1C
1E≌△FCE
∴CF=C
1B
1=CB
∴CF∥AD且CF=AD
∴ADFC为平行四边形
∴AC∥DF∵AC?平面B
1DE
DF?平面B
1DE
∴AC∥平面B
1DE…12分.
分析:(I)根据正方体的几何特征,我们易得三棱锥A-BDE的体积等于三棱锥E-ABD,根据已知中正方体的棱长AA
1=2,E为棱CC
1的中点,求分三棱锥的底面积和高,即可得到三棱锥A-BDE的体积;
(Ⅱ) 连接A
1C
1,根据正方形对角线互相平分可得B
1D
1⊥A
1C
1,由正方体的几何特征可得B
1D
1⊥CC
1,进而由线面垂直的判定定理得到B
1D
1⊥面A
1C
1CA,再由线面垂直的性质定理得到B
1D
1⊥AE;
(Ⅲ) 证法一:连接AC
1,取AC
1的中点为H,取AC的中点O,连接HO,根据平行四边形判定定理可得四边形HOCE为平行四边形,则AC∥HE,进而根据线面平行的判定定理得到AC∥平面B
1DE;
证法二:延长BC与B
1E延长线交于F,连DF,根据三角形全等的判定定理可得△B
1C
1E≌△FCE,进而证得ADFC为平行四边形,则AC∥DF,进而根据线面平行的判定定理得到AC∥平面B
1DE.
点评:本题考查的知识点是直线与平面垂直的性质,棱锥的体积,直线与平面平行的判定,(I)的关键是利用等体积法,将求三棱锥A-BDE的体积转化为求三棱锥E-ABD,(II)的关键是熟练掌握线面垂直的判定及性质定理,(III)的关键是在平面内找到与AC平行的直线,创造使用线面平行判定定理的条件.

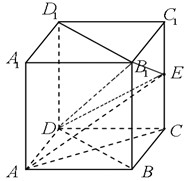 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点. CE.SABD=
CE.SABD= …4分
…4分

 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则