
【题目】已知f(x)=ex﹣ax﹣1.
(1)求f(x)的单调递增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围.
【答案】
(1)解:f′(x)=ex﹣a,令f′(x)≥0,解得ex≥a.
当a≤0时,有f′(x)>0在R上恒成立,此时函数f(x)在R上单调递增;
当a>0时,x≥lna,此时函数f(x)在[lna,+∞)上单调递增
(2)解:f(x)在定义域R内单调递增,
∴f′(x)=ex﹣a≥0恒成立,即a≤ex,x∈R恒成立.
∵x∈R,∴ex∈(0,+∞),∴a≤0.
当a=0时,f′(x)=ex>0在R上恒成立.
故当a≤0时,f(x)在定义域R内单调递增
【解析】(1)f′(x)=ex﹣a,令f′(x)≥0,解得ex≥a.对a分类讨论,即可得出.(2)f(x)在定义域R内单调递增,可得f′(x)=ex﹣a≥0恒成立,即a≤ex , x∈R恒成立.即可得出.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】一个不透明的袋子装有4个完全相同的小球,球上分别标有数字为0,1,2,2,现甲从中摸出一个球后便放回,乙再从中摸出一个球,若摸出的球上数字大即获胜(若数字相同则为平局),则在甲获胜的条件下,乙摸1号球的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的半径分别2 cm和5 cm,圆台的母线长是12 cm,求圆锥SO的母线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中错误的是( )
A.在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样
B.对一个样本容量为100的数据分组,各组的频数如下:
区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的58%
C.设产品产量与产品质量之间的线性相关系数为﹣0.91,这说明二者存在着高度相关
D.通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表:
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() ,则有99%以上的把握认为“选择过马路方式与性别有关”
,则有99%以上的把握认为“选择过马路方式与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=a﹣x2( ![]() ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为: ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.3与3x2+2ax+b=0具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
D.若该大学某女生身高增加1cm,则其体重约增加0.85kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图,则( ) 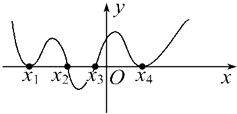
A.函数f(x)有1个极大值点,1个极小值点
B.函数f(x)有2个极大值点,2个极小值点
C.函数f(x)有3个极大值点,1个极小值点
D.函数f(x)有1个极大值点,3个极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣1,1),且同时满足下列条件:
①f(x)是奇函数;
②f(x)在定义域上单调递减;
③f(1﹣a)+f(1﹣a2)<0.
求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com