
【题目】已知函数f(x)的定义域为(﹣1,1),且同时满足下列条件:
①f(x)是奇函数;
②f(x)在定义域上单调递减;
③f(1﹣a)+f(1﹣a2)<0.
求a的取值范围.
【答案】解:由f(1﹣a)+f(1﹣a2)<0得f(1﹣a)<﹣f(1﹣a2),
∵函数y=f(x)是奇函数,
∴﹣f(1﹣a2)=f(a2﹣1),
即不等式等价为f(1﹣a)<f(a2﹣1),
∵y=f(x)在定义域(﹣1,1)上是减函数,
∴有  ,即
,即 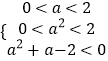 ,
,
∴ 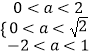 ,解得0<a<1.
,解得0<a<1.
故答案为:0<a<1.

【解析】利用函数是奇函数,将不等式f(1﹣a)+f(1﹣a2)<0转化为f(1﹣a)<﹣f(1﹣a2)=f(a2﹣1),然后利用函数的单调性进行求解.
【考点精析】关于本题考查的函数单调性的判断方法和函数的奇偶性,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1 , x2 , …,xn , 有 ![]() ≤f(
≤f( ![]() ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +x2=1(a>1)与抛物线C
+x2=1(a>1)与抛物线C ![]() :x2=4y有相同焦点F1 .
:x2=4y有相同焦点F1 .
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)已知直线l1过椭圆C1的另一焦点F2 , 且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABCD与等边△ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=AD=2,F为线段EA上的点,且EA=3EF. 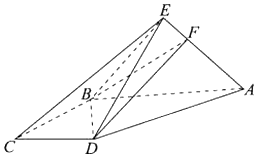
(I)求证:EC∥平面FBD
(Ⅱ)求多面体EFBCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x∈R,记不超过x的最大整数为[x],例如[2.34]=2,[﹣1.5]=﹣2,令{x}=x﹣[x],则 ![]() ( )
( )
A.是等差数列但不是等比数列
B.既是等差数列也是等比数列
C.是等比数列但不是等差数列
D.既不是等差数列也不是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2 , |AB|=4,|F1F2|=2 ![]() ,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.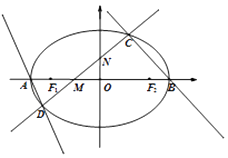
(Ⅰ)求椭圆E的离心率;
(Ⅱ)若m>0,设直线AD、BC的斜率分别为k1、k2 , 求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com