
【题目】已知![]() , 若函数
, 若函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() , 令
, 令![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)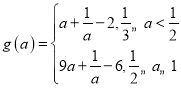 ;(2)实数
;(2)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)根据![]() 解析式,讨论
解析式,讨论![]() 的取值范围,求出
的取值范围,求出![]() 的最值,得出
的最值,得出![]() (a)的表达式;
(a)的表达式;
(2)先用定义判断函数![]() (a)在定义域上的单调性,再求出
(a)在定义域上的单调性,再求出![]() (a)的值域,把方程
(a)的值域,把方程![]() (a)
(a)![]() 有解转化为
有解转化为![]() (a)有解,求出
(a)有解,求出![]() 的取值范围即可.
的取值范围即可.
(1)![]()
![]() 1分
1分
∵![]() ,∴
,∴![]()
①当![]() ,即
,即![]() 时,则
时,则![]() 时,函数
时,函数![]() 取得最大值;
取得最大值;![]() 时,函数
时,函数![]() 取得最小值.
取得最小值.
∴![]() ,
,![]()
∴![]()
![]()
![]() 3分
3分
②当![]() ,即
,即![]() 时,则
时,则![]() 时,函数
时,函数![]() 取得最大值;
取得最大值;![]() 时,函数
时,函数![]() 取得最小值.
取得最小值.
∴![]() ,
,![]()
∴![]()
![]()
![]() . 5分
. 5分
综上,得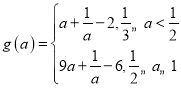
(2)任取![]() ,且
,且![]()
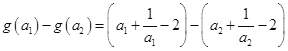
![]() ,
,
∵![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() ;
;
∴![]() ,即
,即![]()
∴![]()
∴函数![]() 在
在![]() 上单调递减 ,
上单调递减 ,
任取![]() ,且
,且![]()
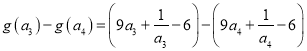
![]()
∵![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() ;
;
∴![]() ,即
,即![]()
∴![]()
∴函数![]() 在
在![]() 上单调递增 ,
上单调递增 ,
当![]() 时,
时,![]() 取得最小值,其值为
取得最小值,其值为![]()
![]()
又![]()
![]() ,
,![]()
![]()
∴函数![]() 的值域为
的值域为![]()
∵关于![]() 的方程
的方程![]() 有解等价于
有解等价于![]() 有解
有解
∴实数![]() 的取值范围为函数
的取值范围为函数![]() 的值域,
的值域,
∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次不等式ax2+x+b>0的解集为(-∞,-2)∪(1,+∞).
(Ⅰ)求a和b的值;
(Ⅱ)求不等式ax2-(c+b)x+bc<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
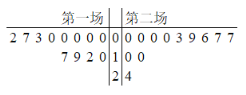
A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是![]() ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用![]() 表示张同学答对题的个数,求
表示张同学答对题的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: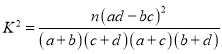 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)已知c>0,关于x的不等式:x+|x-2c|≥2的解集为R.求实数c的取值范围;
(Ⅱ)若c的最小值为m,又p、q、r是正实数,且满足p+q+r=3m,求证:p2+q2+r2≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() 且离心率为
且离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,![]() 的取值范围为
的取值范围为![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,设圆![]() 是圆心在椭圆
是圆心在椭圆![]() 上且半径为
上且半径为![]() 的动圆,过原点
的动圆,过原点![]() 作圆
作圆![]() 的两条切线,分别交椭圆于
的两条切线,分别交椭圆于![]() ,
,![]() 两点.是否存在
两点.是否存在![]() 使得直线
使得直线![]() 与直线
与直线![]() 的斜率之积为定值?若存在,求出
的斜率之积为定值?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com