
分析 (1)当a=1时,分类讨论$f(x)=\left\{\begin{array}{l}{3x-2,x≥1}\\{x,-1<x<1}\\{-3x-4,x≤-1}\end{array}\right.$,求解不等式f(x)>2的解集即可;
(2)由f(x)>b-|x-a2|,得到|x-a2|+|2x+$\frac{2}{{a}^{2}}$|-3>b-|x-a2|,然后利用基本不等式求解即可.
解答 解:(1)当a=1时,$f(x)=\left\{\begin{array}{l}{3x-2,x≥1}\\{x,-1<x<1}\\{-3x-4,x≤-1}\end{array}\right.$,
∴不等式f(x)>2的解集为(-∞,-2)∪($\frac{4}{3}$,+∞);
(2)∵f(x)>b-|x-a2|,
∴|x-a2|+|2x+$\frac{2}{{a}^{2}}$|-3>b-|x-a2|,
∴$2(|x-{a}^{2}|+|x+\frac{1}{{a}^{2}}|)-3>b$.
又∵$2(|x-{a}^{2}|+|x+\frac{1}{{a}^{2}}|)≥2({a}^{2}+\frac{1}{{a}^{2}})-3$$≥4\sqrt{{a}^{2}×\frac{1}{{a}^{2}}}-3=1$,
∴b<1,故实数b的取值范围(-∞,1).
点评 本题考查了绝对值不等式的解法,考查了基本不等式的运用,考查了分类讨论的思想方法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $-\frac{3}{4}$ | C. | $-\frac{5}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
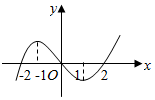
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-2,-1)∪(1,2) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
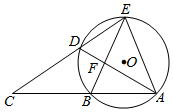 如图,点A,B,D,E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.
如图,点A,B,D,E在⊙O上,ED、AB的延长线交于点C,AD、BE交于点F,AE=EB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若A和B独立,则$\overline{A}$和$\overline{B}$也一定独立 | B. | 若P(A)+P($\overline{B}$)=0.2,则P($\overline{A}$)+P(B)=1.8 | ||
| C. | 若A和B互斥,则必有P(A|B)=P(B|A) | D. | 若A和B独立,则必有P(A|B)=P(B|A) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
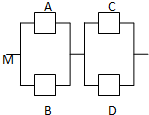 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为0.5、0.6、0.7、0.8.则元件连接成的系统M正常工作的概率P(M)=0.308.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为0.5、0.6、0.7、0.8.则元件连接成的系统M正常工作的概率P(M)=0.308.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com