
| A. | 若A和B独立,则$\overline{A}$和$\overline{B}$也一定独立 | B. | 若P(A)+P($\overline{B}$)=0.2,则P($\overline{A}$)+P(B)=1.8 | ||
| C. | 若A和B互斥,则必有P(A|B)=P(B|A) | D. | 若A和B独立,则必有P(A|B)=P(B|A) |
分析 利用对立、互斥事件,条件概率公式进行判断,即可得出结论.
解答 解:A:A和B独立,则P($\overline{AB}$)=P($\overline{A+B}$)
=1-P(A+B)=1-P(A)-P(B)+P(AB)=[1-P(A)][1-P(B)]=P($\overline{A}$)P($\overline{B}$)
∴$\overline{A}$和$\overline{B}$也一定独立,故A正确;
B:∵P(A)+P($\overline{B}$)+P($\overline{A}$)+P(B)=2,∴P($\overline{A}$)+P(B)=2-0.2=1.8,故B正确;
C:∵P(A|B)=$\frac{P(AB)}{P(B)}$,P(B|A)=$\frac{P(AB)}{P(A)}$,A,B互斥,∴P(AB(=0,∴C正确;
D:∵A和B独立,∴P(A|B)=P(A),P(B|A)=P(B),∴D错误,
故选D.
点评 本题主要考查了概率的基本性质,以及对立事件、互斥事件,条件概率的概念,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{1}{2}$)>f(a2+a+1) | B. | f(-$\frac{1}{2}$)≤f(a2+a+1) | C. | f(-$\frac{1}{2}$)≥f(a2+a+1) | D. | f(-$\frac{1}{2}$)<f(a2+a+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
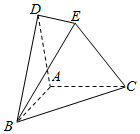 如图,过点A的线段AB,AC,AD在点A处两两垂直,点E为直线BC外一点.
如图,过点A的线段AB,AC,AD在点A处两两垂直,点E为直线BC外一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABEF中,AB∥EF,AF⊥BF,O,M分别是AB,FC的中点,矩形ABCD所在的平面与ABEF所在的平面互相垂直,且AB=2,AD=EF=1.
如图,梯形ABEF中,AB∥EF,AF⊥BF,O,M分别是AB,FC的中点,矩形ABCD所在的平面与ABEF所在的平面互相垂直,且AB=2,AD=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com