练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．集合A={2，0，1，6}，B={x|x+a＞0，x∈R}，A⊆B，则实数a的取值范围是（0，+∞）．

    分析 B={x|x+a＞0，x∈R}=（-a，+∞），又A⊆B，可得-a＜0，解出即可得出．

    解答 解：B={x|x+a＞0，x∈R}=（-a，+∞），
    又A⊆B，∴-a＜0，∴a＞0．
    故答案为：（0，+∞）．

    点评 本题考查了集合之间的关系、不等式的解法，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．设随机事件A，B的对立事件为$\overline{A}$，$\overline{B}$，且P（A）P（B）≠0，则下列说法错误的是（　　）
    A．若A和B独立，则$\overline{A}$和$\overline{B}$也一定独立B．若P（A）+P（$\overline{B}$）=0.2，则P（$\overline{A}$）+P（B）=1.8
    C．若A和B互斥，则必有P（A|B）=P（B|A）D．若A和B独立，则必有P（A|B）=P（B|A）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在△ABC中，已知$\overrightarrow{CD}=2\overrightarrow{BD}$，若$\overrightarrow{AD}=λ\overrightarrow{AB}+u\overrightarrow{AC}$，λ，u∈R，则λu=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

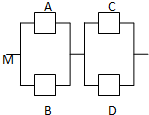    1．如图，用A、B、C、D表示四类不同的元件连接成系统M．当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时，系统M正常工作．已知元件A、B、C、D正常工作的概率依次为0.5、0.6、0.7、0.8．则元件连接成的系统M正常工作的概率P（M）=0.308．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=4sinxcos（x+$\frac{π}{6}$）+1．
    （1）求函数f（x）的单调递减区间；
    （2）在△ABC，角A，B，C的对边分别为a，b，c，若f（A）=2，a=3，S△ABC=$\sqrt{3}$，求b2+c2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．明代程大位《算法统宗》卷10中有题：“远望巍巍塔七层，红灯点点倍加增，共灯三百八十一，请问尖头儿盏灯？”你的答案是（　　）
    A．2盏B．3盏C．4盏D．7盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若用反证法证明命题：三角形的内角中至少有一个大于60°，则与命题结论相矛盾的假设为（　　）
    A．假设三角形的3个内角都大于60°
    B．假设三角形的3个内角都不大于60°
    C．假设三角形的3个内角中至多有一个大于60°
    D．假设三角形的3个内角中至多有两个大于60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．直线x+y+a=0半圆与y=$\sqrt{1-{x^2}}$有两个不同的交点，则a的取值范围是（　　）
    A．[1，$\sqrt{2}$）B．[1，$\sqrt{2}$]C．[-$\sqrt{2}$，1]D．（-$\sqrt{2}$，-1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若a、b满足条件3+log2a=2-log2b（a＞0，b＞0），则$\frac{1}{a}$+$\frac{1}{b}$的最小值为2$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案