
| A. | [1,$\sqrt{2}$) | B. | [1,$\sqrt{2}$] | C. | [-$\sqrt{2}$,1] | D. | (-$\sqrt{2}$,-1] |
分析 数形结合来求,因为曲线y=$\sqrt{1-{x^2}}$表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分.只要把斜率是1的直线平行移动,看a为何时直线与曲线y=$\sqrt{1-{x^2}}$有两个交点即可.
解答 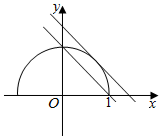 解;曲线y=$\sqrt{1-{x^2}}$表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分.
解;曲线y=$\sqrt{1-{x^2}}$表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分.
作出曲线y=$\sqrt{1-{x^2}}$的图象,在统一坐标系中,再作出斜率是1的直线,由左向右移动,
可发现,直线先与圆相切,再与圆有两个交点,
求出相切时的a值为:-$\sqrt{2}$,最后有两个交点时的a值为-1,
则-$\sqrt{2}$<a≤-1.
故选:D.
点评 此题考查了直线与圆的位置关系,以及函数零点与方程根的关系,利用了数形结合的思想,做出两函数的图象是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
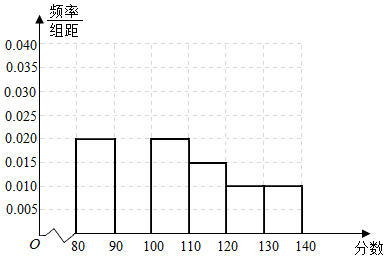
| 组数 | 分组 | 男生 | 占本组的频率 |
| 第一组 | [80,90) | 12 | 0.6 |
| 第二组 | [90,100) | 10 | p |
| 第三组 | [100,110) | 10 | 0.5 |
| 第四组 | [110,120) | a | 0.4 |
| 第五组 | [120,130) | 3 | 0.3 |
| 第六组 | [130,140] | 6 | 0.6 |
| 成绩 性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e-1] | B. | $[\frac{1}{e}+1,e-1]$ | C. | $[\frac{1}{e}+1,2]$ | D. | [0,e-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com