已知数列{an}的前n项和为Sn,对任意n∈N*,有2an=Sn+n.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设f(n)=n2 (n∈N*),试比较Sn与f(n)的大小,并说明理由.
解:(Ⅰ)当n=1时,2a
1=a
1+1∴a
1=1…(1分)
∵2a
n=S
n+n,n∈N
*,∴2a
n-1=S
n-1+n-1,n≥2,
两式相减得a
n=2a
n-1+1,n≥2,即a
n+1=2(a
n-1+1),n≥2,
令b
n=a
n+1,则
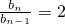
,n≥2且b
1=a
1+1=2,
所以b
n=b
1•2
n-1=2×2
n-1=2
n.n∈N
*,
∴a
n=2
n-1,n∈N
*…(7分)
(Ⅱ)由(Ⅰ)a
n=2
n-1,n∈N
*,
得S
n=(2+2
2+2
3+…+2
n)-n
=
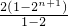
-n
=2
n+1-n-2
当n=1,2时,S
n=f(n);当n≥3时,S
n>f(n)…(9分)
只需证2
n+1>n
2+n+2,n≥3,
利用
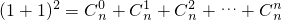
>
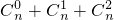
=
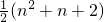
.
∴2
n+1>n
2+n+2,n≥3.…(13分)
分析:(Ⅰ)通过已知条件构造新数列,求出新数列的通项公式,然后求数列{a
n}的通项公式;
(Ⅱ)求出S
n,通过比较n=1,2,比较S
n与f(n)的大小,猜想n≥3时的结果,利用二项式定理证明即可.
点评:本题考查数列通项公式的求法,二项式定理证明不等式的应用,考查计算能力,转化思想;也可用数学归纳法证,也可构造函数s(x)=2
x+1,f(x)=x
2+x+2,利用导数证明,方法比较多.

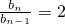 ,n≥2且b1=a1+1=2,
,n≥2且b1=a1+1=2,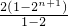 -n
-n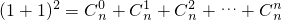 >
>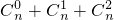 =
=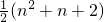 .
.
