
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ∥
∥![]() ,
,![]() ,平面
,平面![]() ⊥底面
⊥底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)在棱![]() 上是否存在点
上是否存在点![]() 使得二面角
使得二面角![]() 大小为
大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)证明见解析;(2)答案见解析.
【解析】试题分析:
(Ⅰ)要证面面垂直,就要证线面垂直,题中由已知可得BD⊥AD,再由面面垂直的性质可得BQ⊥平面PAD,从而可得面面垂直;
(Ⅱ)假设存在,以Q为原点建立解析中所示的空间直角坐标系. 写出各点坐标,同时设 ![]() ,且
,且![]() ,得
,得![]() ,求出平面MBQ,平面CBQ的法向量,由法向量的夹角与二面角的关系求出
,求出平面MBQ,平面CBQ的法向量,由法向量的夹角与二面角的关系求出![]() ,若求出不出
,若求出不出![]() ,则说明不存在,求出则说明存在.
,则说明不存在,求出则说明存在.
试题解析:
(Ⅰ)∵AD // BC,BC=![]() AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD // BQ .
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ![]() 平面PQB,∴平面PQB⊥平面PAD.
平面PQB,∴平面PQB⊥平面PAD.
(Ⅱ)假设存在点点![]() 使得二面角
使得二面角![]() 大小为
大小为![]()
∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以 平面BQC的法向量为![]()
由 ![]() ,且
,且![]() ,得
,得![]()
又![]() ,
,
设平面MBQ法向量![]()
则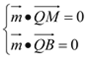
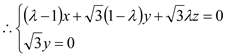
![]() 取
取![]() ∴ 平面MBQ法向量为
∴ 平面MBQ法向量为![]() .
.
∵二面角M-BQ-C为30°, 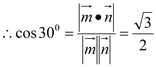
即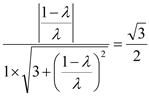 解得
解得 ![]() .
.
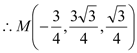 ∴
∴![]()
![]()
所以 存在点M满足![]() 时,二面角
时,二面角![]() 大小为
大小为![]() ,
,
且QM的长度为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点为
)的左焦点为![]() ,左准线方程为
,左准线方程为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若直线![]() 经过椭圆
经过椭圆![]() 的左焦点
的左焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() ,
, ![]() .求证:
.求证: ![]() 为定值;
为定值;
②若![]() (
(![]() 为原点),求
为原点),求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]已知函数f(x)=|2x﹣a|+a.
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣1|,当x∈R时,f(x)+g(x)≥3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( ) 参考数据: ![]() ,sin15°≈0.2588,sin7.5°≈0.1305.
,sin15°≈0.2588,sin7.5°≈0.1305.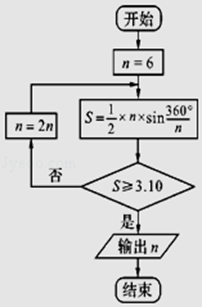
A.12
B.24
C.48
D.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0)为双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
=1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.x2﹣ ![]() =1
=1
C.x2﹣y2=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com