
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若曲线![]() 上点
上点![]() 处的切线过点
处的切线过点![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(Ⅱ)若函数![]() 在
在![]() 上无零点,求
上无零点,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由导数几何意义得切线斜率,再由点斜式得切线方程,代入点![]() 可解得
可解得![]() ,再根据函数
,再根据函数![]() 导函数小于零,解得单调减区间;(Ⅱ)先由题意得
导函数小于零,解得单调减区间;(Ⅱ)先由题意得![]() ,
,![]() 恒成立,再变量分离转化为对应函数最值:
恒成立,再变量分离转化为对应函数最值:![]() 的最大值,最后利用导数求函数
的最大值,最后利用导数求函数![]() ,
,![]() 最大值,经过二次求导可得
最大值,经过二次求导可得![]() 在区间
在区间![]() 内为增函数,
内为增函数,![]() ,因此
,因此![]() .
.
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,所以函数
,所以函数![]() 的单调减区间为
的单调减区间为![]() .
.
(Ⅱ)因为当![]() →
→![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 内恒成立不可能. 所以要使函数
内恒成立不可能. 所以要使函数![]() 在区间
在区间![]() 内无零点,只要对任意的
内无零点,只要对任意的![]() ,
,![]() 恒成立,即对
恒成立,即对![]() ,
,![]() 恒成立.
恒成立.
令![]() ,
,![]() ,则
,则![]() .
.
再令![]() ,
,![]() ,则
,则![]()
![]()
![]() ,
,
所以![]() 在区间
在区间![]() 内为减函数,所以
内为减函数,所以![]() ,
,
∴![]() .
.
于是![]() 在区间
在区间![]() 内为增函数,所以
内为增函数,所以![]() ,
,
所以要使![]() 恒成立,只要
恒成立,只要![]() .
.
综上,若函数![]() 在区间
在区间![]() 内无零点,则实数
内无零点,则实数![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了![]() 人,得到如下的统计表和频率分布直方图.
人,得到如下的统计表和频率分布直方图.
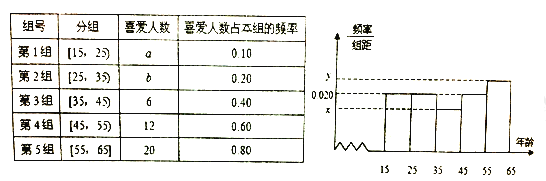
(1)写出其中![]() 及
及![]() 和
和![]() 的值;
的值;
(2)若从第1,2,3,组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求抽取的2人年龄都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() , 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
, 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
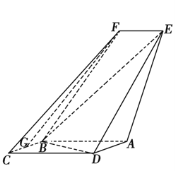
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x﹣m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)﹣ax+1,a为实常数,求g(x)在区间[﹣1,1]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
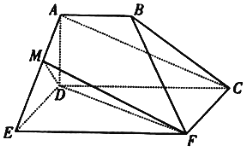
【题目】如图所示,空间几何体![]() 中,四边形
中,四边形![]() 是梯形,四边形
是梯形,四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)求证: ![]() ;
;
(2)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(3)在(2)的条件下,求空间几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com