
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C到平面A1BD的距离.

(1)证明过程见解析;(2)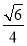 ;(3)
;(3)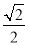
【解析】
试题分析:(1)取 中点
中点 ,连结
,连结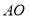 ,取
,取 中点
中点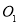 ,以
,以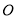 为原点,
为原点,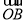 ,
,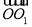 ,
, 的方向为
的方向为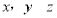 轴的正方向建立空间直角坐标系,写出
轴的正方向建立空间直角坐标系,写出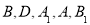 坐标,进而得出向量坐标,利用向量垂直时坐标关系可证明
坐标,进而得出向量坐标,利用向量垂直时坐标关系可证明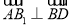 ,
,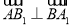 ,可得
,可得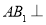 平面
平面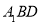 ;(2)令平面
;(2)令平面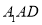 的法向量为
的法向量为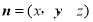 ,则
,则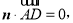
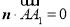 ,可得一法向量
,可得一法向量 ,由(1)
,由(1)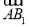 为平面
为平面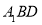 的法向量,那么二面角的余弦值即为
的法向量,那么二面角的余弦值即为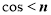 ,
, ;(3)可求
;(3)可求 ,
,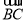 .
.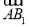 为平面
为平面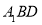 的法向量,所以C到平面A1BD的距离
的法向量,所以C到平面A1BD的距离 .
.
【解析】
(1)取 中点
中点 ,连结
,连结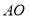 .
.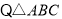 为正三角形,
为正三角形,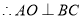 ,
,
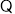 在正三棱柱
在正三棱柱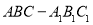 中,平面
中,平面 平面
平面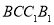 ,
,
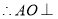 平面
平面 ,
,

取 中点
中点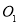 ,以
,以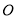 为原点,
为原点,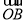 ,
,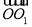 ,
, 的方向为
的方向为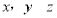 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
,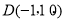 ,
, ,
,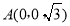 ,
,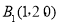 ,
,
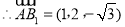 ,
,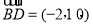 ,
,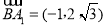 .
.
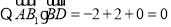 ,
,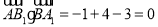 ,
,
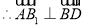 ,
,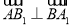 ,
,
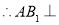 平面
平面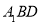 . 4分
. 4分
(2)设平面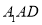 的法向量为
的法向量为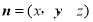 ,
,
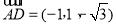 ,
,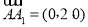 ,
,
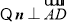 ,
,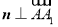 ,
,

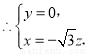
令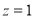 得
得 为平面
为平面 的一个法向量,
的一个法向量,
由(1)知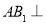 平面
平面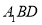 ,
, 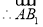 为平面
为平面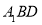 的法向量,
的法向量,
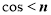 ,
,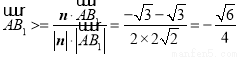 ,
,
 二面角
二面角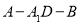 的余弦值为
的余弦值为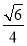 . 9分
. 9分
(3)由(2),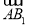 为平面
为平面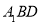 法向量,
法向量,
 ,
,
 点
点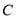 到平面
到平面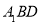 的距离
的距离 . 12分
. 12分
考点:空间向量的应用,线面垂直的判定.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源:2015届新疆兵团农二师华山中学高二下学期期中理科数学试卷(解析版) 题型:选择题
设集合 ,那么“
,那么“ ”是“
”是“ ”的
”的
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林十八中高二下学期开学考文科数学试卷(解析版) 题型:选择题
在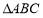 中,
中,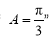 是
是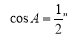 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:填空题
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.

查看答案和解析>>
科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试理科数学试卷(解析版) 题型:选择题
设a>0,b>0,则以下不等式中不一定成立的是( )
A.a2+b2+2≥2a+2b B.
C. +
+ ≥2 D.a3+b3≥2ab2
≥2 D.a3+b3≥2ab2
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林中学高二下学期期中考试文科数学试卷(解析版) 题型:选择题
函数 ,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
A.20 B.18 C.3 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com