Question

11．已知命题：
①将一组数据中的每个数都变为原来的2倍，则方差也变为原来的2倍；
②命题“?x∈R，x²+x+1＜0”的否定是“?x∈R，x²+x+1＜0”；
③在△ABC中，若A＞B，则sinA＜sinB；
④在正三棱锥S-ABC内任取一点P，使得V_P-ABC＜$\frac{1}{2}$V_S-ABC的概率是$\frac{7}{8}$；
⑤若对于任意的n∈N⁺，n²+（a-4）n+3+a≥0恒成立，则实数a的取值范围是[$\frac{1}{3}$，+∞）．
以上命题中正确的是③④⑤（填写所有正确命题的序号）．

Answer 1

分析 根据方差是刻画数据离散程度的量，可判断①；根据特称命题否定的方法，可判断②；根据正弦定理③；根据几何概型可判断④；根据孤立参数法，构造函数求出a的范围，可判断⑤．

解答 解：①将一组数据中的每个数都变为原来的2倍，则方差也变为原来的2²=4倍，故错误；
②命题“?x∈R，x²+x+1＜0”的否定是“?x∈R，x²+x+1≤0”，故错误；
③在△ABC中，若A＞B，则a＞b，则2RsinA＞2RsinB，则sinA＞sinB，故错误；
④如图所示，O是正△ABC的中心，分别取棱SA，SB，SC的中点D，E，F，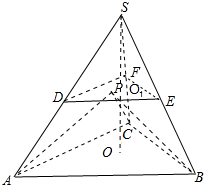

则在△DEF及其内部任取一点P，则V_P-ABC=$\frac{1}{3}$S_△ABC×$\frac{1}{2}$SO=$\frac{1}{2}$V_S-ABC，
因此使得使得V_P-ABC＜$\frac{1}{2}$V_S-ABC的概率是1-$\frac{{V}_{S-DEF}}{{V}_{S-ABC}}$=$\frac{7}{8}$，故正确；
⑤若对于任意的n∈N^*，n²+（a-4）n+3+a≥0恒成立，则a≥-$\frac{{n}^{2}-4n+3}{n+1}$=-（n+1+$\frac{8}{n+1}$-6），
令f（x）=x+$\frac{8}{x}$（x≥2），f′（x）=1-$\frac{8}{{x}^{2}}$，
当x≥3时，f′（x）＞0，函数f（x）单调递增，
∴f（x）≥f（3）=3+$\frac{8}{3}$=5$\frac{2}{3}$，
f（4）=6，当x=2时，f（2）=6，
∴a≥-（5$\frac{2}{3}$-6）=$\frac{1}{3}$，
∴实数a的取值范围是[$\frac{1}{3}$，+∞），故正确；
故正确的命题为：③④⑤，
故答案为：③④⑤

点评 本题考查了简易逻辑的判定方法、方差的性质、正弦定理、三棱锥的体积、特殊命题的否定，考查了推理能力与计算能力，属于中档题．