
分析 (Ⅰ)求出M,N的坐标,利用|OM|2+|ON|2=8求曲线E的方程;
(Ⅱ)利用点差法,求出CD的斜率,即可证明结论.
解答 (Ⅰ)解:设P(m,n),直线$PM:y-n=\frac{{\sqrt{3}}}{2}({x-m})$,令y=0,得$M({m-\frac{{2\sqrt{3}}}{3}n,0})$,
直线$PN:y-n=-\frac{{\sqrt{3}}}{2}({x-m})$,令y=0,得$N({m+\frac{{2\sqrt{3}}}{3}n,0})$.
∴${\overrightarrow{OM}^2}+{\overrightarrow{ON}^2}={({m-\frac{{2\sqrt{3}}}{3}n})^2}+{({m+\frac{{2\sqrt{3}}}{3}n})^2}=2{m^2}+\frac{{8{n^2}}}{3}=8⇒\frac{m^2}{4}+\frac{n^2}{3}=1$.
∴曲线E的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(Ⅱ)证明:∵AB∥CD,设$\overrightarrow{AQ}=λ\overrightarrow{QC},\overrightarrow{BQ}=λ\overrightarrow{QD},({λ>0})$,A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),
则(1-xA,1-yA)=λ(xC-1,yC-1),
即xA=1+λ-λxC,yA=1+λ-λyC①,同理xB=1+λ-λxD,yB=1+λ-λyD②
将A(xA,yA),B(xB,yB),代入椭圆方程得$\left\{\begin{array}{l}\frac{{{x_A}^2}}{4}+\frac{{{y_A}^2}}{3}=1\\ \frac{{{x_B}^2}}{4}+\frac{{{y_B}^2}}{3}=1\end{array}\right.$,
化简得3(xA+xB)(xA-xB)=-4(yA+yB)(yA-yB)③
把①②代入③,得3(2+2λ)(xC-xD)-3λ(xC+xD)(xC-xD)=-4(2+2λ)(yC-yD)+4λ(2+2λ)(yC+yD)(yC-yD)
将C(xC,yC),D(xD,yD),代入椭圆方程,同理得3(xC+xD)(xC-xD)=-4(yC+yD)(yC-yD)代入上式得3(xC-xD)=-4(yC-yD).
即$\frac{{{y_C}-{y_D}}}{{{x_C}-{x_D}}}=-\frac{3}{4}$,
∴直线AB的斜率为定值$-\frac{3}{4}$
点评 本题考查轨迹方程,考查点差法的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{17}{25}$ | C. | -$\frac{17}{25}$ | D. | $\frac{31}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
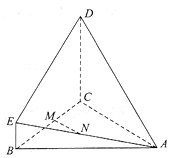 如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.
如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com