
分析 (1)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(2)由x>0,得到$2a≥\frac{lnx-2}{x}$恒成立,令$φ(x)=\frac{lnx-2}{x}$(x>0),根据函数的单调性求出a的范围即可;
(3)求出函数g(x)的导数,通过讨论a的范围,求出函数的单调区间,根据函数的极值得到a的表达式,令$h(x)=-\frac{x^3}{2}-\frac{x}{2}+xlnx+1$,x∈(0,1),根据函数的单调性证明即可.
解答 解:(1)当a=2时,f(x)=lnx-4x,则$f'(x)=\frac{1}{x}-4$(x>0),…(1分)
∴f(1)=-4,f'(1)=-3,…(2分)
∴函数f(x)的图象在x=1处的切线方程为y-(-4)=-3×(x-1),
即3x+y+1=0. …(3分)
(2)不等式f(x)≤2,即lnx-2ax≤2,∴2ax≥lnx-2,
∵x>0,∴$2a≥\frac{lnx-2}{x}$恒成立,…(4分)
令$φ(x)=\frac{lnx-2}{x}$(x>0),则$φ'(x)=\frac{3-lnx}{x^2}$,
当0<x<e3时,φ'(x)>0,φ(x)单调递增,
当x>e3时,φ'(x)<0,φ(x)单调递减,
∴当x=e3时,φ(x)取得极大值,也为最大值,
故$φ{(x)_{max}}=φ({e^3})=\frac{1}{e^3}$,…(5分)
由$2a≥\frac{1}{e^3}$,得$a≥\frac{1}{{2{e^3}}}$,
∴实数a的取值范围是$[\frac{1}{{2{e^3}}},+∞)$. …(6分)
(3)证明:由$g(x)=f(x)+\frac{1}{2}{x^2}=\frac{1}{2}{x^2}-2ax+lnx$,
得$g'(x)=x+\frac{1}{x}-2a=\frac{{{x^2}-2ax+1}}{x}$,…(7分)
①当-1≤a≤1时,g'(x)≥0,g(x)单调递增无极值点,不符合题意;…(8分)
②当a>1或a<-1时,令g'(x)=0,设x2-2ax+1=0的两根为x0和x',
∵x0为函数g(x)的极大值点,∴0<x0<x',
由x0•x'=1,x0+x'=2a>0,知a>1,0<x0<1,
又由$g'({x_0})={x_0}+\frac{1}{x_0}-2a=0$,得$a=\frac{{{x_0}^2+1}}{{2{x_0}}}$,…(9分)
∵${x_0}f({x_0})+1+a{x_0}^2={x_0}ln{x_0}-\frac{{{x_0}^3+{x_0}}}{2}+1$(0<x0<1),
令$h(x)=-\frac{x^3}{2}-\frac{x}{2}+xlnx+1$,x∈(0,1),则$h'(x)=-\frac{{3{x^2}}}{2}+\frac{1}{2}+lnx$,
令$μ(x)=-\frac{{3{x^2}}}{2}+\frac{1}{2}+lnx$,x∈(0,1),则$μ'(x)=-3x+\frac{1}{x}=\frac{{1-3{x^2}}}{x}$,
当$0<x<\frac{{\sqrt{3}}}{3}$时,μ'(x)>0,当$\frac{{\sqrt{3}}}{3}<x<1$时,μ'(x)<0,
∴$μ{(x)_{max}}=μ(\frac{{\sqrt{3}}}{3})=ln\frac{{\sqrt{3}}}{3}<0$,…(11分)
∴h'(x)<0,∴h(x)在(0,1)上单调递减,∴h(x)>h(1)=0,
∴${x_0}f({x_0})+1+a{x_0}^2>0$. …(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查转化思想,分类讨论思想,是一道综合题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2018}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
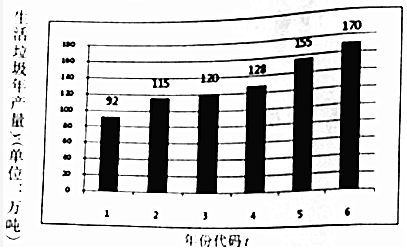
| 2016年初 | 2016年末 | |
| 社区A | 539 | 568 |
| 社区B | 543 | 585 |
| 社区C | 568 | 600 |
| 社区D | 496 | 513 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20种 | B. | 30种 | C. | 40种 | D. | 60种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )
一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1),(0,1,1),($\frac{1}{2}$,1,0),绘制该四面体三视图时,按照如图所示的方向画正视图,则得到左视图可以为( )| A. | 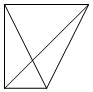 | B. | 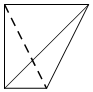 | C. | 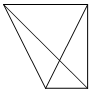 | D. | 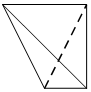 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com