
| 2016年初 | 2016年末 | |
| 社区A | 539 | 568 |
| 社区B | 543 | 585 |
| 社区C | 568 | 600 |
| 社区D | 496 | 513 |
分析 (1)计算$\overline{t}$,$\overline{y}$,代入回归方程求出$\overline{a}$,得出回归方程,再令t=10计算2020年生活垃圾的产生量;
(2)①计算2016年的参与度增加值,得出2017年的参与度增加值的百分比,从而得出2017年的生活垃圾无害化处理量;
②计算2016到2020年参与度增加量的百分比,计算2020年的生活垃圾无害化处理量,与2020年的生活垃圾的产生量比较大小即可得出结论.
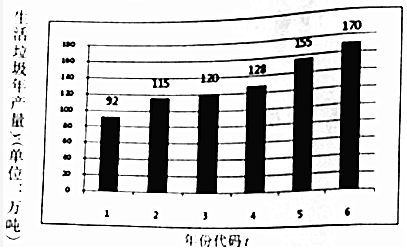
解答 解:(1)由图知,$\overline{t}$=$\frac{1}{6}$×(1+2+3+4+5+6)=3.5,
$\overline{y}$=$\frac{1}{6}$×(92+115+120+128+155+170)=130;
∴130=14.8×3.5+$\overline{a}$,∴$\widehat{a}$=130-14.8×3.5=78.2,
∴回归直线方程为$\widehat{y}$=14.8t+78.2,
令x=10,计算$\widehat{y}$=14.8×10+78.2=226.2,
∴预测2020年该年生活垃圾的产生量为226.2吨.
(2)①2016年初的参与度为$\frac{539+543+568+496}{1000×4}$=0.5365,
2016年末的参与度为$\frac{568+585+600+513}{1000×4}$=0.5665,
∴2016年该市参与度的年增加值为0.5665-0.5365=0.03.
∴2017年的参与度年增加值为0.03,即增加3个百分点,
∴2017年全市生活垃圾无害化处理量为120+6×3=138万吨.
②2020年的参与度相比2016年增加18个百分点,
∴2020年的全市生活垃圾无害化处理量为120+18×6=228万吨,
∵228>226.2,
∴到2020年该市能实现生活垃圾无害化处理率达到100%的目标.
点评 本题考查了数据统计处理,线性回归方程的求解与预测,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
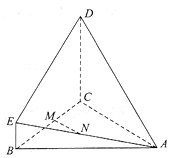 如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.
如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | [1,5) | C. | (4,5) | D. | [4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 0.1 | 1.8 | m | 4 |
| A. | 2.9 | B. | 3.1 | C. | 3.5 | D. | 3.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com