练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知变量x，y具有线性相关关系，它们之间的一组数据如下表所示，若y关于x的线性回归方程为$\stackrel{∧}{y}$=1.3x-1，则m的值为（　　）
    x1234
    y0.11.8m4
    A．2.9B．3.1C．3.5D．3.8

    分析 利用线性回归方程经过样本中心点，即可求解．

    解答 解：由题意，$\overline{x}$=2.5，代入线性回归方程为$\stackrel{∧}{y}$=1.3x-1，可得$\overline{y}$=2.25，
    ∴0.1+1.8+m+4=4×2.25，
    ∴m=3.1．
    故选B．

    点评 本题考查线性回归方程经过样本中心点，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．若二次函数f（x）=ax2+bx+c（a≤b）的值域为[0，+∞），则$\frac{b-a}{a+b+c}$的最大值是$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

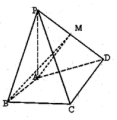    5．在四棱锥P-ABCD中，PA⊥AD，PA=1，PC=PD，底面ABCD是梯形，AB∥CD，AB⊥BC，AB=BC=1，CD=2．
    （1）求证：PA⊥AB；
    （2）设M为PD的中点，求三棱锥M-PAB的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．城市发展面临生活垃圾产生量逐年剧增的困扰，为了建设宜居城市，2017年1月，某市制定《生活垃圾分类和减量工作方案》，到2020年，生活垃圾无害化处理率达到100%．如图是该市2011～2016年生活垃圾年产生量（单位：万吨）的柱状图；如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表：

    2016年初2016年末
    社区A539568
    社区B543585
    社区C568600
    社区D496513
    注1：年份代码1～6分别对应年份2011～2016
    注2：参与度=$\frac{参加垃圾分类人数}{调查人数}$×100%
    参与度的年增加值=年末参与度-年初参与度
    （1）由图可看出，该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系，运用最小二乘法可得回归直线方程为$\widehat{y}$=14.8t+$\widehat{a}$，预测2020年该年生活垃圾的产生量；
    （2）已知2016年该市生活在垃圾无害化化年处理量为120万吨，且全市参与度每提高一个百分点，都可使该市的生活垃圾无害化处理量增加6万吨，用样本估计总体的思想解决以下问题：
    ①由表的数据估计2016年该市参与度的年增加值，假设2017年该市参与度的年增加值与2016年大致相同，预测2017年全市生活垃圾无害化处理量；
    ②在2017年的基础上，若2018年至2020年的参与度逐年增加5个百分点，则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知数列{an} 满足a1=$\frac{1}{3}$，a2=$\frac{2}{3}$，an+2-an+1=（-1）n+1（an+1-an）（n∈N*），数列{an}的前n项和为Sn，则S2017=$\frac{4033}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．甲、乙、丙3位志愿者安排在周一至周六的六天中参加某项志愿者活动，要求每人参加一天且每天至多安排一人，并要求甲安排在另外两位前面，不同的安排放法共有（　　）
    A．20种B．30种C．40种D．60种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知公比q≠1的等比数列{an}前n项和Sn，a1=1，S3=3a3，则S5=（　　）
    A．1B．5C．$\frac{31}{48}$D．$\frac{11}{16}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知f（x）=|2x+3|-|2x-1|．
    （Ⅰ）求不等式f（x）＜2的解集；
    （Ⅱ）若存在x∈R，使得f（x）＞|3a-2|成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合A={x|y=lg（x+1）}，B={-2，-1，0，1}，则（∁RA）∩B=（　　）
    A．{-2，-1}B．{-2}C．{-1，0，1}D．{0，1}

    查看答案和解析>>

    同步练习册答案