
分析 设b-a=k,由△=0,可得c=$\frac{(a+k)^{2}}{4a}$,$\frac{b-a}{a+b+c}$=$\frac{k}{2a+k+c}$=$\frac{k}{2a+k+\frac{(a+k)^{2}}{4a}}$=$\frac{k}{\frac{9a}{4}+\frac{3k}{2}+\frac{{k}^{2}}{4a}}$=$\frac{1}{\frac{9a}{4k}+\frac{k}{4a}+\frac{3}{2}}$,再利用基本不等式求得它的最大值.
解答 解:设b-a=k,则b=a+k,
且△=b2-4ac=(a+k)2-4ac=0,
∴c=$\frac{(a+k)^{2}}{4a}$.
∴$\frac{b-a}{a+b+c}$=$\frac{k}{2a+k+c}$=$\frac{k}{2a+k+\frac{(a+k)^{2}}{4a}}$
=$\frac{k}{\frac{9a}{4}+\frac{3k}{2}+\frac{{k}^{2}}{4a}}$=$\frac{1}{\frac{9a}{4k}+\frac{k}{4a}+\frac{3}{2}}$≤$\frac{1}{2\sqrt{\frac{9a}{4k}•\frac{k}{4a}}+\frac{3}{2}}$=$\frac{1}{2×\frac{3}{4}+\frac{3}{2}}$=$\frac{1}{3}$,
当且仅当k=3a,b=4a时,取得最大值$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查二次函数的性质,基本不等式的应用,注意用放缩法,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
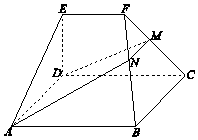 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{17}{25}$ | C. | -$\frac{17}{25}$ | D. | $\frac{31}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{b}$|=2 | B. | |2$\overrightarrow{a}-\overrightarrow{b}$|=2$\sqrt{3}$ | C. | 2$\overrightarrow{a}•\overrightarrow{b}$=-2 | D. | $\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 0.1 | 1.8 | m | 4 |
| A. | 2.9 | B. | 3.1 | C. | 3.5 | D. | 3.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com