
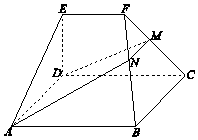
 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.分析 (Ⅰ)通过证明AD∥BC,推出AD∥平面FBC,然后证明平AD∥MN.
(Ⅱ)证明AD⊥CD,结合AD⊥FC,说明AD⊥平面CDEF,然后证明平面ADMN⊥平面CDEF.
(Ⅲ)说明DA,DC,DE两两互相垂直,建立空间直角坐标系D-xyz,不妨设EF=ED=1,求出相关的坐标,求出平面FBC的法向量,平面ADE的法向量,通过向量的数量积求解二面角A-l-B的平面角的大小即可.
解答  (本小题满分14分)
(本小题满分14分)
(Ⅰ)证明:因为ABCD为矩形,所以AD∥BC,[(1分)]
所以AD∥平面FBC.[(3分)]
又因为平面ADMN∩平面FBC=MN,
所以AD∥MN.[(4分)]
(Ⅱ)证明:因为ABCD为矩形,所以AD⊥CD.[(5分)]
因为AD⊥FC,[(6分)]
所以AD⊥平面CDEF.[(7分)]
所以平面ADMN⊥平面CDEF.[(8分)]
(Ⅲ)解:因为EA⊥CD,AD⊥CD,
所以CD⊥平面ADE,
所以CD⊥DE.
由(Ⅱ)得AD⊥平面CDEF,
所以AD⊥DE.
所以DA,DC,DE两两互相垂直.[(9分)]
建立空间直角坐标系D-xyz.[(10分)]
不妨设EF=ED=1,则CD=2,设AD=a(a>0).
由题意得,A(a,0,0),B(a,2,0),C(0,2,0),D(0,0,0),E(0,0,1),F(0,1,1).
所以$\overrightarrow{CB}$=(a,0,0),$\overrightarrow{CF}$=(0,-1,1).
设平面FBC的法向量为$\overrightarrow{n}$=(x,y,z),则
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CB}=0}\\{\overrightarrow{n}•\overrightarrow{CF}=0}\end{array}\right.$即$\left\{{\begin{array}{l}{ax=0}\\{-y+z=0}\end{array}}\right.$令z=1,则y=1.
所以$\overrightarrow{n}$=(0,1,1).[(12分)]
又平面ADE的法向量为$\overrightarrow{DC}$=(0,2,0),所以
$|cos<\overrightarrow{n},\overrightarrow{DC}>|$=$\frac{|\overrightarrow{n}•\overrightarrow{DC}|}{|\overrightarrow{n}||\overrightarrow{DC}|}$=$\frac{\sqrt{2}}{2}$.
因为二面角A-l-B的平面角是锐角,
所以二面角A-l-B的大小45°.[(14分)]
点评 本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
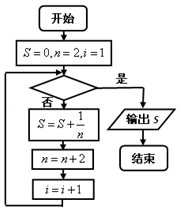
| A. | i>1009? | B. | i<1009? | C. | i>2018? | D. | i<2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,log2x≥2x+3 | B. | ?x>0,log2x≥2x+3 | C. | ?x>0,log2x<2x+3 | D. | ?x<0,log2x≥2x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
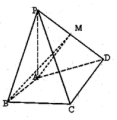 在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com