
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}$ |
分析 由题意可得PF1⊥PF2,|PO|=$\frac{1}{2}$|F1F2|=c,求出双曲线的一条渐近线方程,可得x0,y0的方程,解方程可得P的坐标,解直角三角形PAB,可得b=2a,求出a,c的关系,运用离心率公式即可得到所求值.
解答  解:F1,F2为其左右焦点,满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,
解:F1,F2为其左右焦点,满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,
可得PF1⊥PF2,|PO|=$\frac{1}{2}$|F1F2|=c,
由双曲线的渐近线方程y=-$\frac{b}{a}$x,
即有x02+y02=c2,bx0+ay0=0,
解得P(-a,b),
则PA⊥AB,
又∠PBF1=45°,
则|PA|=|AB|,
即有b=2a,可得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a,
则e=$\frac{c}{a}$=$\sqrt{5}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程和直角三角形的性质,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
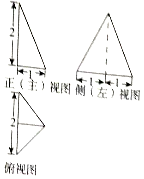
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
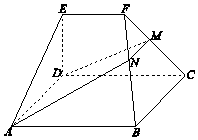 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com