
 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.分析 (Ⅰ)取PB的中点F,连接AF,EF,证明:四边形ADEF是平行四边形,可得DE∥AF,即可证明ED∥面PAB;
(Ⅱ)取BC的中点M,连接AM,面PAC内做PH⊥AC于H,又面PAC⊥面ABCD,且面PAC∩面ABCD=AC,所以PH⊥面ABCD,即可求点P到面ABCD的距离.
解答 (Ⅰ)证明:取PB的中点F,连接AF,EF.(1分)
因为EF是△PBC的中位线,所以$EF\underline{\underline{∥}}\frac{1}{2}BC$.(2分)
又$AD\underline{\underline{∥}}\frac{1}{2}BC$,所以$AD\underline{\underline{∥}}EF$,所以四边形ADEF是平行四边形.(3分)
所以DE∥AF,又DE?面ABP,AF?面ABP,所以ED∥面PAB.(5分)
(Ⅱ)解:取BC的中点M,连接AM,则$AD\underline{\underline{∥}}MC$,
所以四边形ADCM是平行四边形.
所以AM=MC=MB,所以A在以BC为直径的圆上.(6分)
所以AB⊥AC,可得$AC=\sqrt{3}$.(7分)
因为面PAC⊥面ABCD,且面PAC∩面ABCD=AC,
所以AB⊥面PAC,(8分)
即AB⊥PA,可得$PA=\sqrt{3}$.(9分)
在面PAC内做PH⊥AC于H,又面PAC⊥面ABCD,且面PAC∩面ABCD=AC,所以PH⊥面ABCD.(10分)
由余弦定理可得$cos∠PAC=\frac{{P{A^2}+C{A^2}-P{C^2}}}{2•PA•CA}=\frac{1}{3}$,所以$sin∠PAC=\frac{{2\sqrt{2}}}{3}$.(11分)$PH=PA•sin∠PAC=\frac{{2\sqrt{6}}}{3}$,即P到面ABCD的距离为$\frac{{2\sqrt{6}}}{3}$.(12分)
点评 本题考查线面平行的判定,考查点面距离的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 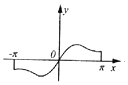 | C. | 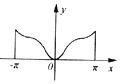 | D. | 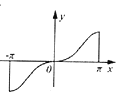 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,log2x≥2x+3 | B. | ?x>0,log2x≥2x+3 | C. | ?x>0,log2x<2x+3 | D. | ?x<0,log2x≥2x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com