
 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.分析 (Ⅰ)证明:CD⊥平面EAD,即可证明ED⊥CD;
(Ⅱ)证明AD∥平面FBC,即可证明:AD∥MN;
(Ⅲ)若使平面ADMN⊥平面BCF,则DM⊥平面BCF,所以DM⊥FC,可得DF=DC=2.若使DM⊥FC能成立,则M为FC的中点.
解答 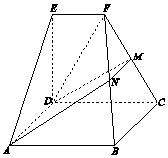 (Ⅰ)证明:因为ABCD为矩形,所以VD⊥AD.[(1分)]
(Ⅰ)证明:因为ABCD为矩形,所以VD⊥AD.[(1分)]
又因为CD⊥EA,[(2分)]
所以CD⊥平面EAD.[(3分)]
所以ED⊥CD.[(4分)]
(Ⅱ)证明:因为ABCD为矩形,所以AD∥BC,[(5分)]
所以AD∥平面FBC.[(7分)]
又因为平面ADMN∩平面FBC=MN,
所以AD∥MN.[(8分)]
(Ⅲ)解:平面ADMN与平面BCF可以垂直.证明如下:[(9分)]
连接DF.因为AD⊥ED,AD⊥CD.ED∩CD=D,
所以AD⊥平面CDEF.[(10分)]
所以AD⊥DM.
因为AD∥MN,所以DM⊥MN.[(11分)]
因为平面ADMN∩平面FBC=MN,
若使平面ADMN⊥平面BCF,
则DM⊥平面BCF,所以DM⊥FC.[(12分)]
在梯形CDEF中,因为EF∥CD,DE⊥CD,CD=2EF=2,ED=$\sqrt{3}$,
所以DF=DC=2.
所以若使DM⊥FC能成立,则M为FC的中点.
所以$\frac{FM}{FC}$=$\frac{1}{2}$.[(14分)]
点评 本题考查线面平行的判定与性质,考查线面垂直、面面垂直,考查学生分析解决问题的能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. | 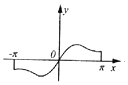 | C. | 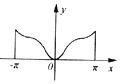 | D. | 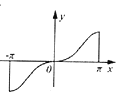 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,log2x≥2x+3 | B. | ?x>0,log2x≥2x+3 | C. | ?x>0,log2x<2x+3 | D. | ?x<0,log2x≥2x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2018}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 2016年初 | 2016年末 | |
| 社区A | 539 | 568 |
| 社区B | 543 | 585 |
| 社区C | 568 | 600 |
| 社区D | 496 | 513 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com