
| A. | |$\overrightarrow{b}$|=2 | B. | |2$\overrightarrow{a}-\overrightarrow{b}$|=2$\sqrt{3}$ | C. | 2$\overrightarrow{a}•\overrightarrow{b}$=-2 | D. | $\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=1 |
分析 以等腰梯形的底AB所在的直线为x轴,以AB的垂直平分线为y轴,建立如图所示的平面直角坐标系,根据题意求出$\overrightarrow{a}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=(2,0),再根据向量的坐标运算和向量的数量积公式和向量的模即可判断.
解答 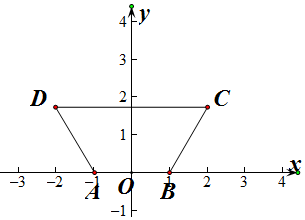 解:以等腰梯形的底AB所在的直线为x轴,以AB的垂直平分线为y轴,建立如图所示的平面直角坐标系,
解:以等腰梯形的底AB所在的直线为x轴,以AB的垂直平分线为y轴,建立如图所示的平面直角坐标系,
∵AB∥DC、CD=2AB=4,∠A=$\frac{2π}{3}$,
∴A(-1,0),B(1,0),C(2,$\sqrt{3}$),D(-2,$\sqrt{3}$),
∴$\overrightarrow{AD}$=2$\overrightarrow{a}$=(-1,$\sqrt{3}$),$\overrightarrow{BC}$=2$\overrightarrow{a}$+$\overrightarrow{b}$=(1,$\sqrt{3}$),
∴$\overrightarrow{a}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=(2,0),
∴|$\overrightarrow{b}$|=2,2$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,$\sqrt{3}$),2$\overrightarrow{a}$•$\overrightarrow{b}$=-1×2+$\sqrt{3}$×0=-2,$\overrightarrow{a}$+$\overrightarrow{b}$=($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)
∴|2$\overrightarrow{a}-\overrightarrow{b}$|=2$\sqrt{3}$,$\overrightarrow{a}$($\overrightarrow{a}$+$\overrightarrow{b}$)=-$\frac{3}{4}$+$\frac{3}{4}$=0,
故选:D.
点评 本题考查了向量的坐标运算和向量的数量积和向量的模,关键是建立坐标系,属于中档题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (2,$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$) | C. | ($\frac{8}{{e}^{2}}$,2) | D. | ($\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
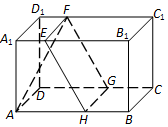 如图,在长方体ABCD-A1B1C1D1中,AB=8,BC=5,AA1=4,平面α截长方体得到一个矩形EFGH,且A1E=D1F=2,AH=DG=5.
如图,在长方体ABCD-A1B1C1D1中,AB=8,BC=5,AA1=4,平面α截长方体得到一个矩形EFGH,且A1E=D1F=2,AH=DG=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
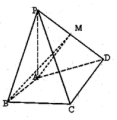 在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四棱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{31}{48}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com