
| A. | (-∞,-2)∪(2,+∞) | B. | (2,$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$) | C. | ($\frac{8}{{e}^{2}}$,2) | D. | ($\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$,+∞) |
分析 利用导数的性质判断f(x)的单调性和极值,得出方程f(x)=t的根的分布情况,从而得出关于t的方程t2-kt+1=0的根的分布情况,利用二次函数函数的性质列不等式求出k的范围.
解答 解:f′(x)=2xex+x2ex=x(x+2)ex,
令f′(x)=0,解得x=0或x=-2,
∴当x<-2或x>0时,f′(x)>0,当-2<x<0时,f′(x)<0,
∴f(x)在(-∞,-2)上单调递增,在(-2,0)上单调递减,在(0,+∞)上单调递增,
∴当x=-2时,函数f(x)取得极大值f(-2)=$\frac{4}{{e}^{2}}$,
当x=0时,f(x)取得极小值f(0)=0.
作出f(x)的大致函数图象如图所示: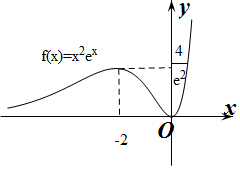
令f(x)=t,则当t=0或t>$\frac{4}{{e}^{2}}$时,关于x的方程f(x)=t只有1解;
当t=$\frac{4}{{e}^{2}}$时,关于x的方程f(x)=t有2解;
当0<t<$\frac{4}{{e}^{2}}$时,关于x的方程f(x)=t有3解.
∵g(x)=f2(x)-kf(x)+1恰有四个零点,
∴关于t的方程t2-kt+1=0在(0,$\frac{4}{{e}^{2}}$)上有1解,在($\frac{4}{{e}^{2}}$,+∞)∪{0}上有1解,
显然t=0不是方程t2-kt+1=0的解,
∴关于t的方程t2-kt+1=0在(0,$\frac{4}{{e}^{2}}$)和($\frac{4}{{e}^{2}}$,+∞)上各有1解,
∴$\frac{16}{{e}^{4}}-\frac{4k}{{e}^{2}}+1<0$,解得k>$\frac{4}{{e}^{2}}+\frac{{e}^{2}}{4}$.
故选D.
点评 本题考查了函数零点与函数图象的关系,函数单调性的判断与极值计算,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
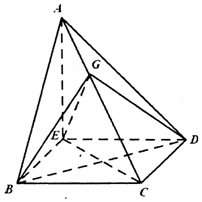 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 65 | C. | 80 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{b}$|=2 | B. | |2$\overrightarrow{a}-\overrightarrow{b}$|=2$\sqrt{3}$ | C. | 2$\overrightarrow{a}•\overrightarrow{b}$=-2 | D. | $\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
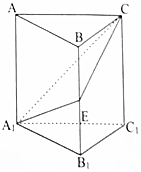 如图,在正三棱柱ABC-A1B1C1中,A1B1=2,AA1=h,E为BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,A1B1=2,AA1=h,E为BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$或$\frac{\sqrt{10}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{10}}{3}$或$\sqrt{10}$ | D. | $\frac{\sqrt{10}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com