练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为

    A．三棱台、三棱柱、圆锥、圆台           B．三棱台、三棱锥、圆锥、圆台  

    C．三棱柱、正四棱锥、圆锥、圆台         D．三棱柱、三棱台、圆锥、圆台

     

    【答案】

    C.

    【解析】

    试题分析：由三视图与几何体之间的对应关系可知（1）（2）（3）（4）依次为三棱柱、正四棱锥、圆锥、圆台.

    考点：空间几何体的三视图.

    点评：掌握常见几何体的三视图是解决这类小题的关键，平时要多画柱、锥、台体的三视图，提高自己的空间想象能力.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

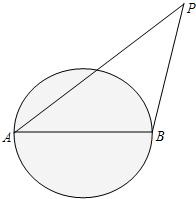    精英家教网外轮除特许外，不得进入离我国海岸线12海里以内的区域，如图：我国某海岛海岸线是半径为6海里的圆形区域，在直径的两个端点A、B设立两个观察点，已知一外轮在点P处，测得∠BAP=α，∠ABP=β．
    （1）当α=30°，β=120°时，该外轮是否已进入我领海主权范围内？
    （2）角α，β应满足什么关系时？就应向外轮发出警告，令其退出我海域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

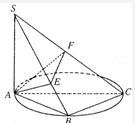    精英家教网如图已知点B在以AC为直径的圆上，SA⊥面ABC，AE⊥SB于E，AF⊥SC于F．
    （1）证明：SC⊥EF；
    （2）若SA=a，∠ASC=
    π
    4
    ，∠AFE=
    π
    6
    ，求三棱锥S-AEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，正方体ABCD-A1B1C1D1的棱长为2，点E在线段BD上，点F在线段B1C上．
    （Ⅰ）若E、F分别为线段BD，B1C的中点，求直线EF与直线C1D1所成的角；
    （Ⅱ）若EF⊥BD，EF⊥B1C，求线段EF的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个空间几何体的三视图如图所示，该几何体的体积为1，则正视图中的x的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

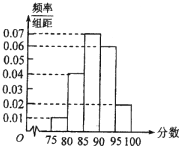    精英家教网某年级1000位学生某次测试成绩的频率分布直方图如图所示，其中成绩分组区间为：[75，80）、[80，85）、[85，90）、[90，95）、[95，100]，规定成绩不低于90分的学生为优秀．
    （l）用分层抽样的方法从这1000人中抽取50人的成绩进行分析，求抽取优秀的学生入数；
    （2）在（1）抽取的样本中，从优秀的学生中任取两人，记“成绩不低于95分的人数”为ξ，求ξ的分布列和期望．

    查看答案和解析>>

    同步练习册答案