
已知函数f(x)=(1-x)ex-1.
(1)求函数f(x)的最大值;
(2)设g(x)= ,x>-1,且x≠0,证明:g(x)<1.
,x>-1,且x≠0,证明:g(x)<1.
解:(1)f′(x)=-xex.
当x∈(-∞,0)时,f′(x)>0,f(x)单调递增;
当x∈(0,+∞)时,f′(x)<0,f(x)单调递减.
所以f(x)的最大值为f(0)=0.
(2)证明:由(1)知,当x>0时,f(x)<0,g(x)= <0<1.
<0<1.
当-1<x<0时,g(x)<1等价于f(x)>x.
设h(x)=f(x)-x,则h′(x)=-xex-1.
当x∈(-1,0)时,0<-x<1,0<ex<1,则0<-xex<1,
从而当x∈(-1,0)时,h′(x)<0,h(x)在(-1,0)上单调递减.
当-1<x<0时,h(x)>h(0)=0,即g(x)<1.
综上,总有g(x)<1.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
如图K132所示,某飞行器在4千米高空水平飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图像的一部分,则该函数的解析式为 ( )
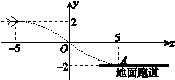
图K132
A.y=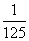 x3-
x3-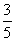 x
x
B.y=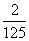 x3-
x3-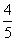 x
x
C.y=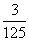 x3-x
x3-x
D.y=-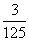 x3+
x3+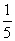 x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
已知不等式ax2+bx+c≥0的解集为[-1,3],则函数f(x)=-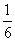 bx3+ax2+cx+m的单调递增区间为( )
bx3+ax2+cx+m的单调递增区间为( )
A.(-∞,-1),(3,+∞)
B.(-1,3)
C.(-3,1)
D.(-∞,-3),(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=aex+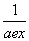 +b(a>0).
+b(a>0).
(1)求f(x)在[0,+∞)上的最小值;
(2)设曲线y=f(x)在点(2,f(2))处的切线方程为y=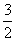 x,求a,b的值.
x,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com