（12分）如图,等边
与直角梯形
垂直,
,
,
,
.若
分别为
的中点.(1)求
的值； (2)求面
与面
所成的二面角大小.
(1)
；
(2)面SCD与面SAB所成的二面角大小为
.
解析试题分析：(1)因为
，然后再在
中求值即可.
(2)利用空间向量法求二面角，要首先求出二面角两个面的法向量然后转化为两个面的法向量的夹角求解.
(1)在正中
,面
面，
面，
，
中，
(也可用坐标计算)………6分
(2)建立如图所示的直角坐标系
则
,
,
设面SCD的法向量为
由
，由
不妨设
则
,
，
，
面SAB的法向量为 
面SCD与面SAB所成的二面角大小为..………12分.
考点：空间几何体的线线，线面，面面垂直的判定与性质，向量的运算，二面角.
点评：（1）本小题在进行向量运算时用到的公式：若M为BC的中点，则
.
(2)在利用空间向量求二面角时首先求出两个面的法向量，同时要注意法向量的夹角与二面角可能相等也可能互补，要注意判断准确.
高效智能课时作业系列答案科目：高中数学 来源： 题型：解答题
（本题满分12分）如图所示，已知四棱锥S—ABCD的底面ABCD是矩形，M、N分别是CD、SC的中点，SA⊥底面ABCD，SA=AD=1，AB=
.
（1）求证：MN⊥平面ABN；（2）求二面角A—BN—C的余弦值
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分14分）
如图, 在直三棱柱
中，
，
,
．
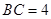（1）求证：
；
（2）问：是否在
线段上存在一点
，使得
平面
？
若存在，请证明；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
本小题满分14分）
如图，在直三棱柱
中，
，
，
，点
、
分别是
、
的中点.
（Ⅰ）求证：
平面
；
（Ⅱ）证明：平面
平面
；
（Ⅲ）求多面体A1B1C1BD的体积V.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
如图，在四棱锥
中，底面
是矩形，
平面，
，
，点
为
的中点，
为
中点.
（1）求证：平面
⊥平面
；
（2）求直线
与平面所成的角的正弦值；
（3）求点到平面的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
点为棱
的中点.
.
，求异面直线
与
所成的角的余弦值.
是矩形，
，
，
为
上的点，且
．
；
．
中，
⊥平面
，
⊥平面
，
。
，
是底
对角线的交点．
面
；
面