
【题目】已知函数![]() ,
, ![]() ,其中a>1.
,其中a>1.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 在点
在点![]() 处的切线平行,证明
处的切线平行,证明![]() ;
;
(III)证明当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线.
的切线.
【答案】(Ⅰ)单调递减区间![]() ,单调递增区间为
,单调递增区间为![]() ;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
【解析】分析:(I)由题意可得![]() .令
.令![]() ,解得x=0.据此可得函数
,解得x=0.据此可得函数![]() 的单调递减区间
的单调递减区间![]() ,单调递增区间为
,单调递增区间为![]() .
.
(II)曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .曲线
.曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .原问题等价于
.原问题等价于![]() .两边取对数可得
.两边取对数可得![]() .
.
(III)由题意可得两条切线方程分别为l1: ![]() .l2:
.l2: ![]() .则原问题等价于当
.则原问题等价于当![]() 时,存在
时,存在![]() ,
, ![]() ,使得l1和l2重合.转化为当
,使得l1和l2重合.转化为当![]() 时,关于x1的方程
时,关于x1的方程![]() 存在实数解,构造函数,令
存在实数解,构造函数,令![]() ,结合函数的性质可知存在唯一的x0,且x0>0,使得
,结合函数的性质可知存在唯一的x0,且x0>0,使得![]() ,据此可证得存在实数t,使得
,据此可证得存在实数t,使得![]() ,则题中的结论成立.
,则题中的结论成立.
详解:(I)由已知, ![]() ,有
,有![]() .
.
令![]() ,解得x=0.
,解得x=0.
由a>1,可知当x变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
x |
| 0 |
|
|
| 0 | + |
|
| 极小值 |
|
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(II)由![]() ,可得曲线
,可得曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
由![]() ,可得曲线
,可得曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
因为这两条切线平行,故有![]() ,即
,即![]() .
.
两边取以a为底的对数,得![]() ,所以
,所以![]() .
.
(III)曲线![]() 在点
在点![]() 处的切线l1:
处的切线l1: ![]() .
.
曲线![]() 在点
在点![]() 处的切线l2:
处的切线l2: ![]() .
.
要证明当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,
的切线,
只需证明当![]() 时,存在
时,存在![]() ,
, ![]() ,使得l1和l2重合.
,使得l1和l2重合.
即只需证明当![]() 时,方程组
时,方程组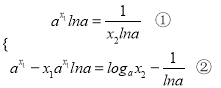 有解,
有解,
由①得![]() ,代入②,得
,代入②,得![]() . ③
. ③
因此,只需证明当![]() 时,关于x1的方程③存在实数解.
时,关于x1的方程③存在实数解.
设函数![]() ,
,
即要证明当![]() 时,函数
时,函数![]() 存在零点.
存在零点.
![]() ,可知
,可知![]() 时,
时, ![]() ;
;
![]() 时,
时, ![]() 单调递减,
单调递减,
又![]() ,
, 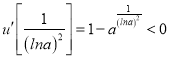 ,
,
故存在唯一的x0,且x0>0,使得![]() ,即
,即![]() .
.
由此可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
因为![]() ,故
,故![]() ,
,
所以![]() .
.
下面证明存在实数t,使得![]() .
.
由(I)可得![]() ,
,
当![]() 时,
时,
有![]()
![]() ,
,
所以存在实数t,使得![]()
因此,当![]() 时,存在
时,存在![]() ,使得
,使得![]() .
.
所以,当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线.
的切线.


科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(m) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
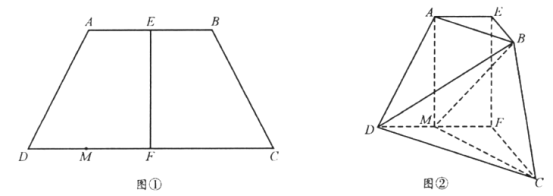
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为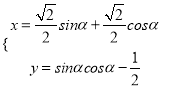 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
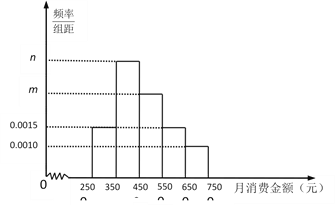
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2名男生、3名女生,全体排成一行,问下列情形各有多少种不同的排法?(以下各题请用数字作答)
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调査了100名市民,统计其周平均网购
的次数,并整理得到如右的频数直方图,将周平均网购次数不小于4次的民众称为网购迷.这100名市民中,年龄不超过40岁的有65人,且网购迷中有5名市民的年龄超过40岁
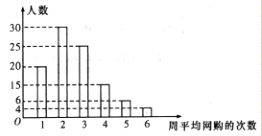
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?

(2)现从网购迷中按分层抽样选5人代表进一步进行调查,若从5人代表中任意挑选2人,求挑选的2人中有年龄超过40岁的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com