
已知A、B、C是直线l上不同的三点,O是l外一点,向量 满足:
满足: 记y=f(x).
记y=f(x).
(1)求函数y=f(x)的解析式:
(2)若对任意 不等式
不等式 恒成立,求实数a的取值范围:
恒成立,求实数a的取值范围:
(3)若关于x的方程f(x)=2x+b在(0,1]上恰有两个不同的实根,求实数b的取值范围.
(1)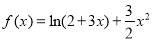 ;(2)
;(2)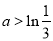 ;(3)
;(3)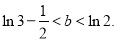 .
.
【解析】
试题分析:(1)根据条件中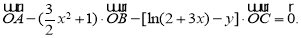 以及A,B,C三点共线可得
以及A,B,C三点共线可得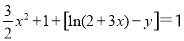 ,从而求得y的解析式;(2)要使
,从而求得y的解析式;(2)要使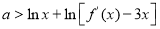 在
在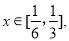 上恒成立,只需
上恒成立,只需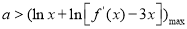 ,通过求导判断
,通过求导判断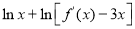 的单调性即可求得
的单调性即可求得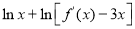 在
在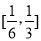 上的最大值,从而得到a的取值范围;(3)题中方程等价于
上的最大值,从而得到a的取值范围;(3)题中方程等价于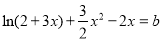 ,因此要使方程有两个不同的实根,只需求得
,因此要使方程有两个不同的实根,只需求得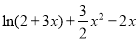 在(0,1]上的取值范围即可,通过求导判断单调性显然可以得到
在(0,1]上的取值范围即可,通过求导判断单调性显然可以得到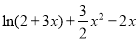 在(0,1]上的取值情况.
在(0,1]上的取值情况.
(1)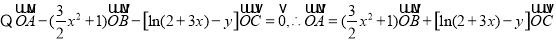 ,
,
又∵A,B,C在同一直线上,∴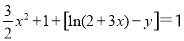 ,则
,则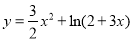 ,
,
∴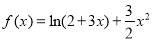 4分
4分
(2) ∴
∴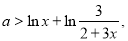 ① 5分
① 5分
设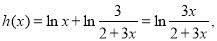 依题意知
依题意知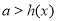 在
在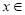
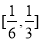 上恒成立,
上恒成立,
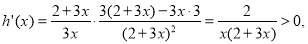 ∴h(x)在
∴h(x)在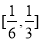 上是增函数,要使不等式①成立,当且仅当
上是增函数,要使不等式①成立,当且仅当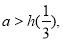 ∴
∴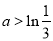 . 8分;
. 8分;
(3)方程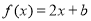 即为
即为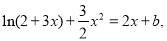 变形为
变形为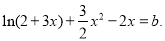
令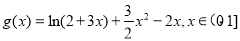 ,
,
∴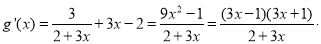 10分
10分
列表写出 x,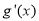 ,
,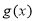 在[0,1]上的变化情况:
在[0,1]上的变化情况:
x |
0 | (0, |
| ( |
1 |
|
| 小于0 | 取极小值 | 大于0 |
|
|
ln2 |
单调递减 |
|
单调递增 |
|
显然?g(x)在(0,1]上的极小值也即为它的最小值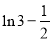 . 12分
. 12分
现在比较ln2与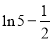 的大小;
的大小;
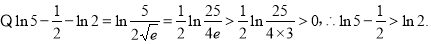
∴要使原方程在(0,1]上恰有两个不同的实根,必须使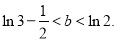
即实数b的取值范围为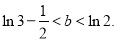 14分.
14分.
考点:1、平面向量共线;2、恒成立问题的处理方法;3、利用导数判断函数单调性求极值.


科目:高中数学 来源:2015届广东省高二下学期中段考理科数学试卷(解析版) 题型:解答题
现有10名教师,其中男教师6名,女教师4名.
(1)要从中选2名教师去参加会议,有多少种不同的选法?
(2)现要从中选出4名教师去参加会议,求男、女教师各选2名的概率.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考理科数学试卷(解析版) 题型:选择题
设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是 ( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com