【答案】
分析:本题考查的是数列与不等式的综合类问题.在解答的过程当中:
(1)首先利用条件和通项与前n项和的关系即可转化出数列a
n的通项之间的关系,进而即可获得数列{a
n}的通项公式;
(2)首先利用第(1)问的结论即可将T
n化简,再利用数学归纳法判断T
n的单调性,由单调性即可获得①的解答,进而由单调性即可获得的最大值从而可以结合②中的恒成立问题进行转化即可获得问题的解答.
解答:解:(1)由题意可知:na
n+1=S
n+n(n+1)
∴(n-1)a
n=S
n-1+(n-1)n
两式相减可得:a
n+1-a
n=2
所以数列{a
n}为以2为首项以2为公差的等差数列.
∴a
n=2+(n-1)•2=2n
∴数列{a
n}的通项公式:a
n=2n,n∈N*
(2)由(1)知:
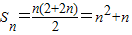
∴
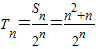
,
∴
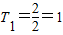
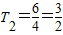
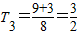
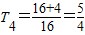
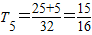
…
可猜测当n≥3时,数列{a
n}为单调递减数列,当n≤2时,数列{a
n}为单调递增数列.
对“当n≥3时,数列{a
n}为单调递减数列”证明如下:
当n=3时,
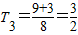
当n=4时,
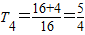
,∴T
4<T
3假设当n=k时成立,即T
k<T
k-1,∴
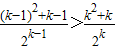
则当n=k+1时,
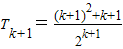
=
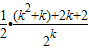
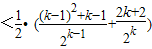
=
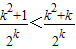
故当n=k+1时猜测成立.综上可知:当n≥3时,数列{a
n}为单调递减数列,当n≤2时,数列{a
n}为单调递增数列.
又因为:对一切正整数n,总有T
n≤m,且T
n的最大值为

,所以
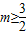
.
∴当n≥3时,T
n>T
n+1,
m的取值范围为:
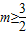
.
点评:本题考查的是数列与不等式的综合类问题.在解答的过程当中充分体现了数列通项与数列前n项和的知识、数列与函数的思想、单调性的研究以及恒成立问题的解答规律.值得同学们体会和反思.

 ,①当n为何值时,Tn>Tn+1,②若对一切正整数n,总有Tn≤m,求m的取值范围.
,①当n为何值时,Tn>Tn+1,②若对一切正整数n,总有Tn≤m,求m的取值范围.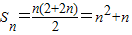
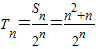 ,
,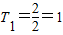
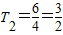
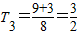
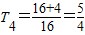
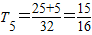
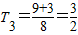
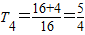 ,∴T4<T3
,∴T4<T3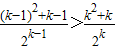
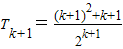 =
=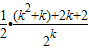
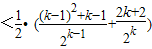
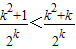
 ,所以
,所以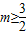 .
.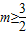 .
.
