
分析 (Ⅰ)设等比数列{an}的公比是q(q≠1),根据等差中项的性质列出方程化简后求出q,由等比数列的通项公式求出an;
(Ⅱ)由(Ⅰ)和条件化简得bn、cn,对n进行依次取值,由正弦函数、余弦函数的性质,分别比较Tn和Pn的大小,由等比数列的特点归纳出结论.
解答 解:(Ⅰ)设等比数列{an}的公比是q(q≠1),
∵a1=$\frac{π}{8}$,且2a2,$\frac{3}{2}$a3,a4成等差数列,
∴2•$\frac{3}{2}$a3=2a2+a4,则$3{a}_{1}{q}^{2}=2{a}_{1}q+{a}_{1}{q}^{3}$,
化简得q2-3q+2=0,解得q=2或q=1(舍去),
∴an=a1•qn-1=$\frac{π}{8}•{2}^{n-1}$=π•2n-4;
(Ⅱ)由(Ⅰ)得,bn=sin$\frac{{2}^{n-1}•π}{8}$,cn=cos$\frac{{2}^{n-1}•π}{8}$,
当n=1时,T1=$sin\frac{π}{8}$,P1=$cos\frac{π}{8}$,则T1<P1;
当n=2时,T2=$sin\frac{π}{8}$+$sin\frac{π}{4}$=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$,P2=$cos\frac{π}{8}$+$cos\frac{π}{4}$=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$,则T2<P2;
当n=3时,T3=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+$sin\frac{π}{2}$=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+1,
P3=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$+$cos\frac{π}{2}$=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$,则T3>P3;
当n=4时,T4=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+$sin\frac{π}{2}$+sinπ=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+1,
P4=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$+$cos\frac{π}{2}$+cosπ=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$-1,则T4>P4;
当n=5时,T5=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+$sin\frac{π}{2}$+sinπ+sin2π=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+1,
P5=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$+$cos\frac{π}{2}$+cosπ+cos2π=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$-1+1=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$,则T5>P5;
当n=6时,T6=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+$sin\frac{π}{2}$+sinπ+sin2π+sin4π=$sin\frac{π}{8}+\frac{\sqrt{2}}{2}$+1,
P6=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$+$cos\frac{π}{2}$+cosπ+cos2π+cos4π=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$-1+1+1=$cos\frac{π}{8}+\frac{\sqrt{2}}{2}$+1,则T6<P6;
…
综上可得,当n=3、4、5时,有Tn>Pn;当n=1、2或n≥6时,有Tn<Pn.
点评 本题考查等比数列的通项公式,等差中项的性质,正弦函数、余弦函数的性质,以及归纳法求数列的和,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | r=1;(-2,1) | B. | r=2;(-2,1) | C. | r=1;(2,-1) | D. | r=2;(2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
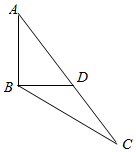 如图,在△ABC中,已知∠ABD=$\frac{π}{2}$,∠CBD=$\frac{π}{6}$,AB=CD=1,则BC=$\root{3}{4}$.
如图,在△ABC中,已知∠ABD=$\frac{π}{2}$,∠CBD=$\frac{π}{6}$,AB=CD=1,则BC=$\root{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com