
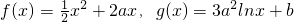 ,其中a>0,设两曲线有公共点P(x0,y0),且在点P(x0,y0)处的切线是同一条直线.
,其中a>0,设两曲线有公共点P(x0,y0),且在点P(x0,y0)处的切线是同一条直线.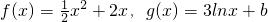
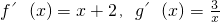 …(2分)
…(2分)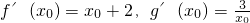 ,且
,且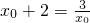 ,解得:x0=-3或1--(4分)
,解得:x0=-3或1--(4分)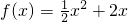 得
得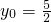 …(6分)
…(6分)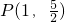 ,…(7分)
,…(7分) …(8分)
…(8分)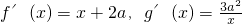 …(10分)
…(10分)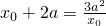 ,即x0=-3a或a,其中x0=-3a舍去…(12分)
,即x0=-3a或a,其中x0=-3a舍去…(12分)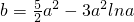 ( a>0)…(13分)
( a>0)…(13分) (t>0)
(t>0)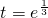 …(14分)
…(14分)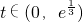
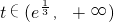 …(15分)
…(15分)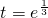 时h(t)取到最大值,即
时h(t)取到最大值,即 ----(16分)
----(16分)

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com