A
分析:设出等差数列的公差为d,由等比数列{a
n}中a
2,a
3,a
4分别是某等差数列的第5项、第3项、第2项,根据等差数列的性质得到等差数列的第五项等于第三项加3d,第三项等于第二项加d,即a
2=a
4+3d,a
3=a
4+d,又a
2,a
3,a
4成等比数列,根据等比数列的性质得到a
32=a
2•a
4,把表示出的a
2和a
3代入,整理后根据公差d不为0,用d表示出a
4,进而用d表示出a
2和a
3,根据等比数列的性质由

求出公比q的值,再由首项a
1的值,利用等比数列的通项公式写出此等比数列的通项公式a
n即可.
解答:设公差为d,根据题意得:
∵等比数列{a
n}中a
2,a
3,a
4分别是某等差数列的第5项、第3项、第2项,
∴a
2=a
4+3d,a
3=a
4+d,
又a
2,a
3,a
4为等比数列{a
n}的项,
∴a
32=a
2•a
4,即(a
4+d)
2=(a
4+3d)a
4(d≠0),
整理得:a
42+2da
4+d
2=a
42+3da
4,即d(d-a
4)=0,
解得:a
4=d,或d=0,
由公比q≠1,得到a
3≠a
4,即d≠0,故d=0舍去,
∴a
4=d,
∴a
2=4d,a
3=2d,
∴q=

=
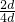
=

,又a
1=1,
则a
n=a
1•q
n-1=

=2
1-n.
故选A
点评:此题考查了等差、等比数列的性质,以及等比数列的通项公式,熟练掌握性质及公式是解本题的关键.

 求出公比q的值,再由首项a1的值,利用等比数列的通项公式写出此等比数列的通项公式an即可.
求出公比q的值,再由首项a1的值,利用等比数列的通项公式写出此等比数列的通项公式an即可. =
=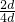 =
= ,又a1=1,
,又a1=1, =21-n.
=21-n.
