
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为
,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为![]() 的正方形.
的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(均不在
两点(均不在![]() 轴上),点
轴上),点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率成等比数列,且
的斜率成等比数列,且![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调査了部分市民(问卷调査表如下表所示),并根据调查结果绘制了尚不完整的统计图表(如下图)

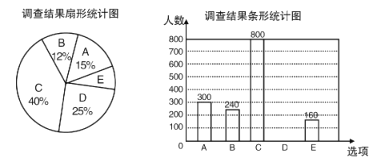
由两个统计图表可以求得,选择D选项的人数和扇形统计图中E的圆心角度数分别为( )
A.500,28.8°B.250,28.6°C.500,28.6°D.250,28.8°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将含有甲、乙、丙的6名医护人员平均分成两组到A、B两家医院参加“防疫救护”工作,则甲、乙至少有一人在A医院且甲、丙不在同一家医院参加“防疫救护”工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C方程为![]() ,椭圆中心在原点,焦点在x轴上.
,椭圆中心在原点,焦点在x轴上.
(1)证明圆C恒过一定点M,并求此定点M的坐标;
(2)判断直线![]() 与圆C的位置关系,并证明你的结论;
与圆C的位置关系,并证明你的结论;
(3)当![]() 时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线
时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线![]() ,
,![]() 的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一位发烧病人的体温记录折线图,下列说法不正确的是( )
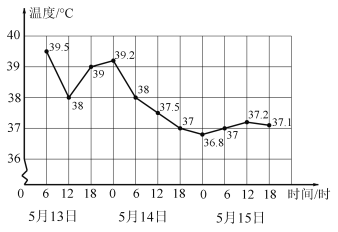
A.病人在5月13日12时的体温是![]()
![]()
B.病人体温在5月14日0时到6时下降最快
C.从体温上看,这个病人的病情在逐渐好转
D.病人体温在5月15日18时开始逐渐稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
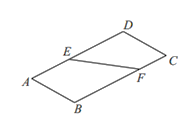
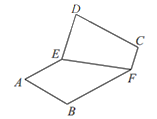
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com