
【题目】已知圆C方程为![]() ,椭圆中心在原点,焦点在x轴上.
,椭圆中心在原点,焦点在x轴上.
(1)证明圆C恒过一定点M,并求此定点M的坐标;
(2)判断直线![]() 与圆C的位置关系,并证明你的结论;
与圆C的位置关系,并证明你的结论;
(3)当![]() 时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线
时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线![]() ,
,![]() 的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
【答案】(1)证明见解析;定点![]() (2)直线与圆C相切;证明见解析;(3)存在;
(2)直线与圆C相切;证明见解析;(3)存在;![]() ,
,![]() 或者
或者![]() ,
,![]()
【解析】
(1)根据题意得到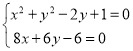 ,解得答案.
,解得答案.
(2)将圆化为标准形式,计算圆心到直线的距离与半径作比较得到答案.
(3)根据准线和椭圆过点计算得到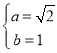 ,得到椭圆方程,设定点
,得到椭圆方程,设定点![]() ,
,![]() ,计算
,计算![]() 为定值,得到
为定值,得到![]() ,计算得到答案.
,计算得到答案.
(1)圆C的方程可化为:![]() ,
,
由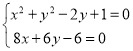 ,解得
,解得![]() ,所以圆C过定点
,所以圆C过定点![]() .
.
(2)圆C的方程可化为:![]() ,
,
圆心到直线l的距离为![]()
![]() ,
,
所以直线与圆C相切.
(3)当![]() 时,圆C方程为
时,圆C方程为![]() ,圆心为
,圆心为![]() ,半径为10,
,半径为10,
与直线![]() ,即
,即![]() 相切,所以椭圆的左准线为
相切,所以椭圆的左准线为![]() ,
,
又椭圆过点![]() ,则
,则![]() ,所以
,所以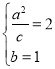 ,解得
,解得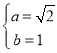 ,
,
所以椭圆方程为![]() .
.
在椭圆上任取一点![]() (
(![]() ),设定点
),设定点![]() ,
,![]() ,
,
则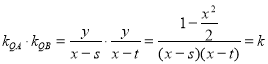 对
对![]() 恒成立,
恒成立,
所以![]() 对
对![]() 恒成立,
恒成立,
所以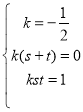 ,故
,故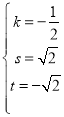 或
或 ,
,
所以![]() ,
,![]() 或者
或者![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数g(x)=sinωx(ω>0)向左平移![]() 个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)在(0,2π)上有且只有3个极大值点,f(x)在(0,2π)上有且只有2个极小值点
C.f(x)在![]() 上单调递增
上单调递增
D.ω的取值范围是[![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
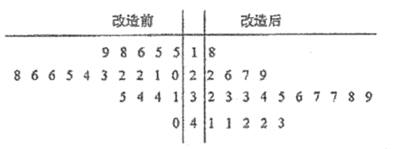
(1)(i)设所采集的40个连续正常运行时间的中位数m,并将连续正常运行时间超过m和不超过m的次数填入下面的列联表:
超过 | 不超过 | |
改造前 | ||
改造后 |
(ii)根据(i)中的列联表,能否有99%的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: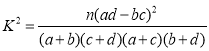
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为T天(即从开工运行到第kT天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:
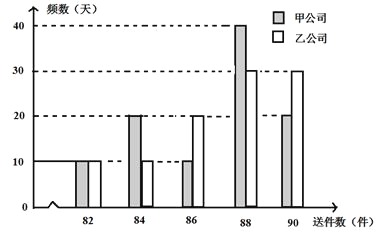
(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得![]() 的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种
的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种![]() 值的表达式纷纷出现,使得
值的表达式纷纷出现,使得![]() 值的计算精度也迅速增加.华理斯在1655年求出一个公式:
值的计算精度也迅速增加.华理斯在1655年求出一个公式:![]() ,根据该公式绘制出了估计圆周率
,根据该公式绘制出了估计圆周率![]() 的近似值的程序框图,如下图所示,执行该程序框图,已知输出的
的近似值的程序框图,如下图所示,执行该程序框图,已知输出的![]() ,若判断框内填入的条件为
,若判断框内填入的条件为![]() ,则正整数
,则正整数![]() 的最小值是
的最小值是
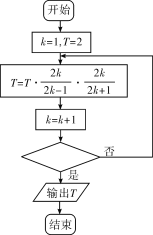
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com