
设等比数列 的首项为
的首项为 ,公比为
,公比为 (
( 为正整数),且满足
为正整数),且满足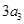 是
是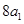 与
与 的等差中项;数列
的等差中项;数列 满足
满足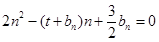 (
(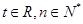 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数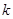 ,在
,在 与
与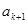 之间插入
之间插入 个2,得到一个新数列
个2,得到一个新数列 . 设
. 设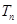 是数列
是数列 的前
的前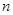 项和,试求满足
项和,试求满足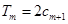 的所有正整数
的所有正整数 .
.
(Ⅰ)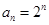 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)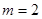
解析试题分析:(Ⅰ)由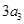 是
是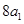 与
与 的等比中项可得
的等比中项可得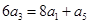 ,根据等比数列基本量可得到关于
,根据等比数列基本量可得到关于 的方程,从而求出
的方程,从而求出 ,由
,由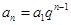 得到数列
得到数列 的通项公式; (Ⅱ)由题中所给
的通项公式; (Ⅱ)由题中所给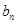 关于
关于 表达式
表达式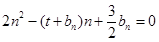 化简得用
化简得用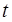 表示
表示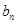 的表达式,即
的表达式,即 ,这样可联想到去求出
,这样可联想到去求出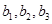 ,利用等差中项可求出
,利用等差中项可求出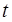 的值,并由此求出
的值,并由此求出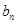 的表达式,最后根据求
的表达式,最后根据求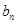 的表达式结合等差数列的定义去证明它是一个等差数列; (Ⅲ)由(Ⅰ)知数列
的表达式结合等差数列的定义去证明它是一个等差数列; (Ⅲ)由(Ⅰ)知数列 的通项公式,由(Ⅱ)知数列
的通项公式,由(Ⅱ)知数列 的通项公式,结合题中要求分析得:
的通项公式,结合题中要求分析得: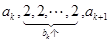 ,
,  ,则可得出数列
,则可得出数列 的大体如下:
的大体如下: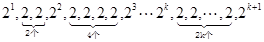 ,可见数列
,可见数列 的前三项均为
的前三项均为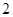 ,由此可验证
,由此可验证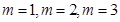 的具体情况,可得其中
的具体情况,可得其中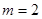 符合题中要求,当
符合题中要求,当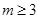 时,分析
时,分析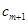 不可能为
不可能为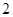 ,因为前面的永大于
,因为前面的永大于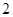 ,那么要存在
,那么要存在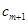 肯定为
肯定为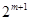 ,这样就可得到关于
,这样就可得到关于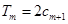 一个假设的等式,并可化简得关于
一个假设的等式,并可化简得关于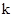 的表达式
的表达式 ,根据特点可设出对应的函数
,根据特点可设出对应的函数 ,最后由导数在函数中的运用去判断出在
,最后由导数在函数中的运用去判断出在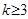 上函数恒为正.
上函数恒为正.
试题解析:解:(Ⅰ)因为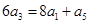 ,所以
,所以 ,
,
解得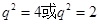 (舍),则
(舍),则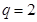 3分
3分
又 ,所以
,所以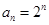 5分
5分
(Ⅱ)由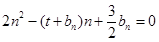 ,得
,得 ,
,
所以 ,
,
则由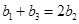 ,得
,得 8分
8分
而当 时,
时,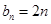 ,由
,由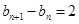 (常数)知此时数列
(常数)知此时数列 为等差数列 10分
为等差数列 10分
(Ⅲ)因为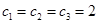 ,易知
,易知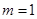 不合题意,
不合题意,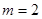 适合题意 11分
适合题意 11分
当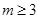 时,若后添入的数2
时,若后添入的数2 ,则一定不适合题意,从而
,则一定不适合题意,从而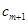 必是数列
必是数列 中的
中的
某一项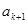 ,则
,则 ,
,
所以 ,即
,即 13分
13分
记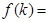
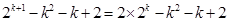 ,则
,则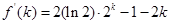 ,
,
因为 ,
,
所以当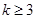 时,
时,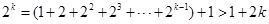 ,又
,又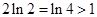 ,
,
从而

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知数列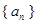 是首项为
是首项为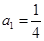 ,公比
,公比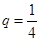 的等比数列.设
的等比数列.设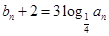 ,
,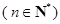 ,数列
,数列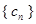 满足
满足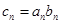 ;
;
(Ⅰ)求证:数列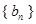 成等差数列;
成等差数列;
(Ⅱ)求数列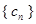 的前
的前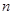 项和
项和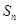 ;
;
(Ⅲ)若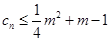 对一切正整数
对一切正整数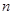 恒成立,求实数
恒成立,求实数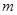 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com