
分析 数列{an}满足an+1-an=2n(n∈N*),a1=3,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1可得an,再利用不等式的性质、数列的单调性即可得出.
解答 解:∵数列{an}满足an+1-an=2n(n∈N*),a1=3,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2×1+3
=2×$\frac{(n-1)n}{2}$+3
=n2-n+3.
则$\frac{a_n}{n}$=$\frac{{n}^{2}-n+3}{n}$=n+$\frac{3}{n}$-1≥$2×\sqrt{n×\frac{3}{n}}$-1=2$\sqrt{3}$-1,等号不成立,当且仅当n=2时,$\frac{{a}_{n}}{n}$的最小值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、基本不等式的性质、“累加求和”方法,考查了推理能力与计算能力,属于中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:选择题
下图是某年我区举行的名师评选活动中,七位评委为某位教师打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为( )
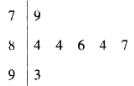
A.84,4.84 B.84,1.6 C.85,1.6 D.85,4
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
若过定点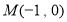 且斜率为
且斜率为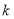 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则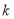 的取值范围是( )
的取值范围是( )
A.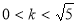 B.
B. C.
C. D.
D.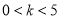
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|-2<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{3}{5}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com