
 在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.分析 (Ⅰ)根据线面垂直的性质定理即可证明BC⊥AD;
(Ⅱ)根据三棱锥的体积公式分别求出两部分的几何体积,即可求平面AEF将三棱锥D-ABC分成两部分的体积之比.
解答 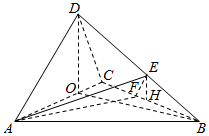 证明:(Ⅰ)∵AD=CD=2,∠BAC=45°,
证明:(Ⅰ)∵AD=CD=2,∠BAC=45°,
∴△ACD是等腰直角三角形,
取AC的中点O,连接OD,
则OD⊥AC,
∵平面ACD⊥平面ABC,
∴OD⊥平面ABC,
则OD⊥BC,
∵AD=CD=2,∠BAC=45°,
∴AC=2$\sqrt{2}$,∵AB=4,∠BAC=45°,
∴BC=2$\sqrt{2}$,
即△ACB是直角三角形,
则BC⊥AC,
∵OD∩AC=0,
∴BC⊥平面ACD,
∵AD?平面ACD,
∴BC⊥AD;
(Ⅱ)由(Ⅰ)得OD=$\sqrt{2}$,
过E作EH⊥平面ABC,
则$\frac{EH}{OD}$=$\frac{BE}{BD}$,
∵BE=2ED,∴$\frac{BE}{BD}$=$\frac{2}{3}$,
则$\frac{EH}{OD}$=$\frac{BE}{BD}$=$\frac{2}{3}$,
则EH=$\frac{2}{3}$OD=$\frac{2\sqrt{2}}{3}$,
∵BC=2BF.
∴F是BC的中点,则BF=$\frac{1}{2}$BC=$\frac{1}{2}$AC=$\frac{1}{2}×2\sqrt{2}$=$\sqrt{2}$,
则△AEF的面积S=$\frac{1}{2}×$BF•AC=$\frac{1}{2}×\sqrt{2}×2\sqrt{2}$=2,
则大三棱锥D-ABC的体积V=$\frac{1}{3}×\frac{1}{2}AC•BC•OD$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}×\sqrt{2}$=$\frac{4\sqrt{2}}{3}$,
三棱锥E-ABF的体积V=$\frac{1}{3}×2×\frac{2\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{9}$,
则另外一部分的体积V=$\frac{4\sqrt{2}}{3}$-$\frac{4\sqrt{2}}{9}$=$\frac{12\sqrt{2}}{9}$-$\frac{4\sqrt{2}}{9}$=$\frac{8\sqrt{2}}{9}$,
则平面AEF将三棱锥D-ABC分成两部分的体积之比为$\frac{8\sqrt{2}}{9}$:$\frac{4\sqrt{2}}{9}$=2.
点评 本题主要考查空间直线和平面位置关系的判断以及三棱锥体积的计算,考查学生的运算和推理能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:解答题
为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
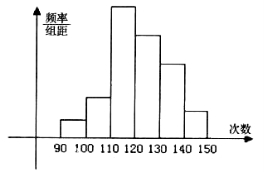
(Ⅰ)求第二小组的频率及样本容量
(Ⅱ)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
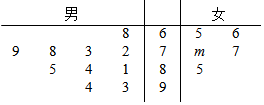 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
下列给出的赋值语句中正确的是( )
A.5 = M B.x =-x C.B=A=3 D.x +y = 7
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com