
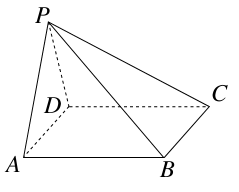
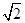 ,CD⊥AB,垂足为D.
,CD⊥AB,垂足为D.
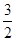
 平面A B1C1,B1C1
平面A B1C1,B1C1 平面A B1C1,∴B1C1∥平面A B1C1;
平面A B1C1,∴B1C1∥平面A B1C1;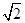 ,
,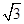 ,又CD⊥AB,∴AC2=AD×AB
,又CD⊥AB,∴AC2=AD×AB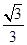 ,AA1=1,∴∠DA1B1=∠A1DA=60°,∠A1B1A=30°,∴AB1⊥A1D
,AA1=1,∴∠DA1B1=∠A1DA=60°,∠A1B1A=30°,∴AB1⊥A1D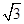 cos30°=
cos30°=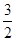 .
.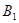 到面
到面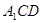 的距离为
的距离为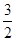 .
. 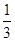 ×
×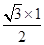 ×
×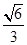 =
=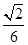 ,而cos∠A1CD=
,而cos∠A1CD=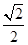 ×
×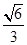 =
=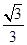 ,
,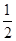 ×
×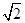 ×
×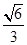 ×
×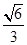 =
=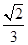 ,设B1到平面A1CD距离为h,则
,设B1到平面A1CD距离为h,则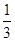 ×
×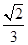 h=
h=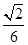 ,得h=
,得h=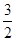 为所求.
为所求.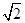 ,0),B1(0,
,0),B1(0,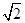 ,1),
,1),
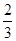 ,
,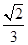 ,0)
,0)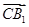 =(0,
=(0,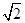 ,1),设平面A1CD的法向量
,1),设平面A1CD的法向量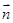 =(x,y,z),则
=(x,y,z),则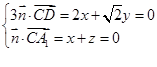 ,取
,取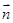 =(1,-
=(1,-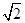 ,-1)
,-1)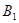 到面
到面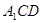 的距离为d=
的距离为d=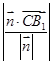
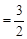


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
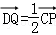 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.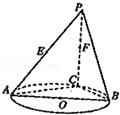
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
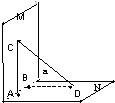
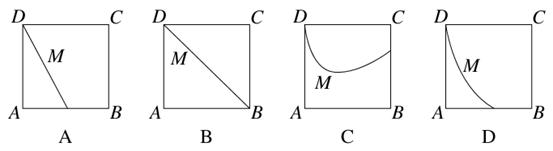
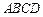 是边长为
是边长为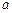 的正方形,
的正方形,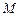 、
、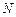 分别是边
分别是边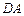 、
、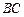 上的点(M不与A、D重合),且
上的点(M不与A、D重合),且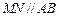 ,
,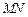 交
交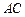 于点
于点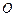 ,沿
,沿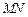 将正方形折成直二面角
将正方形折成直二面角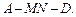
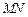 平行移动时,
平行移动时,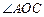 的大小是否发生变化?试说明理由;
的大小是否发生变化?试说明理由;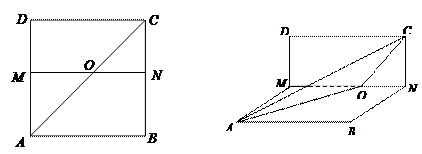 (2)当
(2)当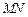 在怎样的位置时,
在怎样的位置时,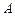 、
、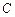 两点间的距离最小?并求出这个最小值.
两点间的距离最小?并求出这个最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com