（推理）三角形的内角和为180º，凸四边形内角和为360º，那么凸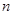
边形的内角和为
A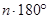． | B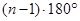． | C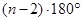． | D． |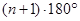
同步练习强化拓展系列答案科目：高中数学 来源： 题型：单选题
用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ）
| A．假设三内角都大于60度； |
| B．假设三内角都不大于60度； |
| C．假设三内角至多有一个大于60度； |
| D．假设三内角至多有两个大于60度。 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
对命题“正三角形的内切圆切于三边的中点”可类比猜想出：正四面体的内切球切于四面都为正三角形的什么位置？（ ）
| A．正三角形的顶点 | B．正三角形的中心 |
| C．正三角形各边的中点 | D．无法确定 |
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
已知点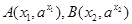
是函数
的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论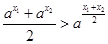
成立．运用类比思想方法可知，若点
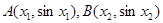是函数
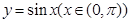的图象上任意不同两点，则类似地有_________________成立．
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“(m·n)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”;
④“t≠0,mt=xt⇒m=x”类比得到“p≠0,a·p=x·p⇒a=x”;
⑤“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑥“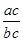
=
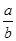”类比得到“
=”.
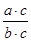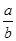以上的式子中,类比得到的结论正确的个数是( )
| A．1 | B．2 | C．3 | D．4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
条时，第一步检验n等于（ ）
是增函数，则
，则
为锐角三角形，则
，则
，第二步证明“从
到
”，左端增加的项数是（ ）
