
对命题“正三角形的内切圆切于三边的中点”可类比猜想出:正四面体的内切球切于四面都为正三角形的什么位置?( )
| A.正三角形的顶点 | B.正三角形的中心 |
| C.正三角形各边的中点 | D.无法确定 |
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:单选题
观察下列事实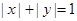 的不同整数解
的不同整数解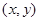 的个数为4,
的个数为4,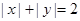 的不同整数解
的不同整数解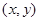 的个数为8,
的个数为8,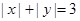 的不同整数解
的不同整数解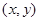 的个数为12,……,则
的个数为12,……,则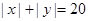 的不同整数解
的不同整数解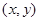 的个数为( )
的个数为( )
| A.76 | B.80 | C.86 | D.92 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“若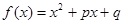 ,那么
,那么 ,
,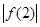 ,
,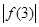 中至少有一个不小于
中至少有一个不小于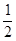 ”时,反设正确的是 ( )
”时,反设正确的是 ( )
A.假设 , ,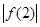 , ,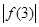 都不小于 都不小于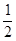 |
B.假设 , ,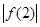 , ,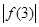 都小于 都小于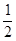 |
C.假设 , ,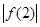 , ,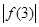 至多有两个小于 至多有两个小于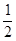 |
D.假设 , ,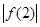 , ,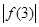 至多有一个小于 至多有一个小于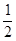 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明不等式“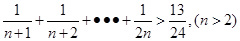 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项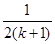 |
B.增加了两项 |
C.增加了一项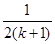 ,又减少了一项 ,又减少了一项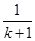 |
D.增加了两项 ,又减少了一项 ,又减少了一项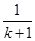 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com