
用数学归纳法证明: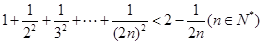 ,第二步证明“从
,第二步证明“从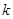 到
到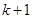 ”,左端增加的项数是( )
”,左端增加的项数是( )
A.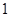 | B.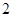 | C.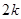 | D.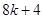 |
科目:高中数学 来源: 题型:单选题
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题“设a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的两根的绝对值都小于1”时,应假设
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明不等式“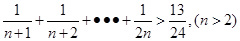 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项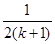 |
B.增加了两项 |
C.增加了一项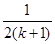 ,又减少了一项 ,又减少了一项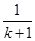 |
D.增加了两项 ,又减少了一项 ,又减少了一项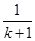 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
由集合{a1},{a1,a2},{a1,a2,a3},…的子集个数归纳出集合{a1,
a2,a3,…,an}的子集个数为( )
| A.n | B.n+1 |
| C.2n | D.2n-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com