
分析 (1)运用数列的递推式:当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1.可得an=n+1;
(2)求得$\frac{(n-1)•{2}^{n}}{n{a}_{n}}$=$\frac{(n-1)•{2}^{n}}{n(n+1)}$=$\frac{{2}^{n+1}}{n+1}$-$\frac{{2}^{n}}{n}$,运用裂项相消求和可得Tn,再由作差法,讨论n的范围,即可得到大小关系.
解答 解:(1)当n=1时,2a1=2S1=(a1-1)(a1+2),
∵a1>0,∴a1=2.
n=2时,2S2=(a2-1)(a2+2)=2(2+a2),
解得a2=3.
当n≥2时,2an=2(Sn-Sn-1)=an2-an-12+an-an-1,
∴(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,∴an-an-1=1,
∴数列{an}是以2为首项,1为公差的等差数列,
∴an=n+1;
(2)解:∵$\frac{(n-1)•{2}^{n}}{n{a}_{n}}$=$\frac{(n-1)•{2}^{n}}{n(n+1)}$=$\frac{{2}^{n+1}}{n+1}$-$\frac{{2}^{n}}{n}$,
∴Tn=$\frac{{2}^{2}}{2}$-$\frac{2}{1}$+$\frac{{2}^{3}}{3}$-$\frac{{2}^{2}}{2}$+…+$\frac{{2}^{n+1}}{n+1}$-$\frac{{2}^{n}}{n}$=$\frac{{2}^{n+1}}{n+1}$-2,
Tn-$\frac{{2}^{n+1}(18-n)-2n-2}{n+1}$=$\frac{{2}^{n+1}}{n+1}$-2-$\frac{{2}^{n+1}(18-n)-2n-2}{n+1}$
=$\frac{{2}^{n+1}(n-17)}{n+1}$,
当n<17且n为正整数时,
$\frac{{2}^{n+1}(n-17)}{n+1}$<0,∴Tn<$\frac{{2}^{n+1}(18-n)-2n-2}{n+1}$;
当n=17时,
$\frac{{2}^{n+1}(n-17)}{n+1}$=0,∴Tn=$\frac{{2}^{n+1}(18-n)-2n-2}{n+1}$;
当n>17且n为正整数时,
$\frac{{2}^{n+1}(n-17)}{n+1}$>0,∴Tn>$\frac{{2}^{n+1}(18-n)-2n-2}{n+1}$.
点评 本题考查等差数列的定义的运用,考查数列的求和方法:裂项相消求和,以及分类讨论思想方法,考查化简整理的运算能力,属于中档题.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 6 | 8 | 10 | 12 | 14 |
| 支出y(万元) | 6 | 7 | 8 | 9 | 10 |
| A. | 15万元 | B. | 14万元 | C. | 11万元 | D. | 10万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 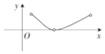 | B. | 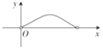 | C. |  | D. | 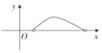 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com