
分析 (Ⅰ)设甲“第一关闯关成功且所得学豆为零”为事件A,“第一关闯关成功第二关闯关失败”为事件A1,“前两关闯关成功第三关闯关失败”为事件A2,则A1,A2互斥,由此能求出选手甲第一关闯关成功且所得学豆为零的概率.
(Ⅱ)X所有可能的取值为0,5,15,35,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)设甲“第一关闯关成功且所得学豆为零”为事件A,
“第一关闯关成功第二关闯关失败”为事件A1,
“前两关闯关成功第三关闯关失败”为事件A2,则A1,A2互斥,
$P({A_1})=\frac{3}{4}×\frac{1}{2}×(1-\frac{2}{3})=\frac{1}{8}$,…(2分)
$P({A_2})=\frac{3}{4}×\frac{1}{2}×\frac{2}{3}×\frac{1}{2}×(1-\frac{1}{2})=\frac{1}{16}$,…(4分)
$P(A)=P({A_1})+P({A_2})=\frac{1}{8}+\frac{1}{16}=\frac{3}{16}$…(5分)
(Ⅱ)X所有可能的取值为0,5,15,35,…(6分)
$P(X=0)=(1-\frac{3}{4})+P(A)=\frac{7}{16}$,
$P(X=5)=\frac{3}{4}×\frac{1}{2}=\frac{3}{8}$,
$P(X=15)=\frac{3}{4}×\frac{1}{2}×\frac{2}{3}×\frac{1}{2}=\frac{1}{8}$,
$P(X=35)=\frac{3}{4}×\frac{1}{2}×\frac{2}{3}×\frac{1}{2}×\frac{1}{2}=\frac{1}{16}$…(10分)
所以,X的分布列为:
| X | 0 | 5 | 15 | 35 |
| P | $\frac{7}{16}$ | $\frac{3}{8}$ | $\frac{1}{8}$ | $\frac{1}{16}$ |
点评 本题考查概率的求法,离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式和互斥事件概率加法公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
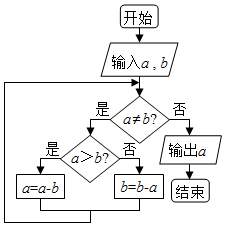 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )| A. | 0 | B. | 2 | C. | 6 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 题号 | A | B | C |
| 答卷份数 | 160 | 240 | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com