
| A. | 4π | B. | 2π | C. | 3π | D. | $\frac{3π}{2}$ |
分析 根据积分的几何意义即可得到结论.
解答 解:设y=$\sqrt{1-\frac{{x}^{2}}{9}}$,(y≥0),
则$\frac{{x}^{2}}{9}$+y2=1(y≥0)对应的曲线为椭圆的上半部分,对应的面积S=$\frac{1}{2}$πab=$\frac{1}{2}×π$×3×1=$\frac{3π}{2}$,
根据积分的几何意义可得$\int_{-3}^3{\sqrt{1-\frac{x^2}{9}}}dx$=$\frac{3π}{2}$.
故选:D.
点评 本题主要考查积分的计算,要求熟练掌握常见函数的积分公式,对于不好求的积分函数,要利用对应的区域面积进行计算.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 命题“?x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
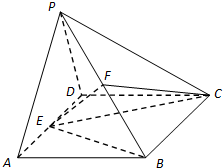 如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.
如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com