
分析 (1)求模应先求出复数的实部与虚部,再利用|a+bi|=$\sqrt{{a}^{2}+{b}^{2}}$得出;
(2)是考查复数几何意义的应用.
解答 解:(1)z 1=i(1-i) 3=i(-2i)(1-i)=2(1-i),
∴|z 1|=$\sqrt{{2}^{2}+{2}^{2}}$=$2\sqrt{2}$.
(2)|z|=1可看成半径为1,圆心为(0,0)的圆,而z 1可看成在坐标系中的点(2,-2),
∴|z-z 1|的最大值可以看成点(2,-2)到圆上点的距离的最大值,由图3-1-3可知,|z-z 1|max=2$\sqrt{2}$+1.
点评 本题考查复数的代数形式混合运算,运用复数的几何意义,采取数形结合的方法解题,可简化解题步骤,事半功倍.也可以在设复数的过程中常设为z=a+bi(a,b∈R );在有关的解决轨迹的问题中常设z=x+yi,从而与解析几何联系起来;当复数的模为1时也可以设为z=cosθ+isinθ,用三角函数解决相关最值等.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | 3π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
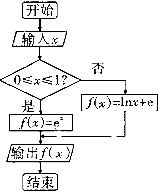 运行如图所示的程序框图,如果在区间[0,e]内任意输入一个x的值,则输出的f(x)值不小于常数e的概率是( )
运行如图所示的程序框图,如果在区间[0,e]内任意输入一个x的值,则输出的f(x)值不小于常数e的概率是( )| A. | $\frac{1}{e}$ | B. | 1-$\frac{1}{e}$ | C. | 1+$\frac{1}{e}$ | D. | $\frac{1}{e+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com