
分析 (1)根据已知条件写出函数f(x)的解析式,结合解析式求得函数f(x)的最小正周期和最大值.
(2)根据正弦函数图象来求函数f(x)的单调递增区间.
解答 解:(1)f(x)=sin2x+cos2x+sinxcosx+cos2x-$\frac{3}{2}$=1+$\frac{1}{2}$sin2x+$\frac{1}{2}$(cos2x+1)-$\frac{3}{2}$=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$).
所以f(x)的最大值为$\frac{\sqrt{2}}{2}$,最小正周期是π.
(2)由(1)知,函数f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$).
所以,该函数的单调递增区间为:-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ⇒-$\frac{3π}{8}$+kπ≤x≤$\frac{π}{8}$+kπ,
所以函数f(x)的单调递增区间为[-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ](k∈Z).
点评 本题考查了数量积运算性质、三角函数的单调性、和差公式、倍角公式、三角次函数的单调性,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
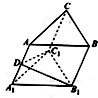 在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.
在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 命题“?x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com